题目内容
如图,在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P是斜边AC上一个动点,D是边BC上一动点,始终有PB=PD,再过D作DE⊥AC于点E.
(1)求证:△BPO≌△PDE.
(2)当点P运动到OA的中点时,求出此时CD:AP的值.
(3)当点P运动到OC的中点时,满足题中条件的点D也随之在直线BC上运动到点D′,请画出此时的图形并直接写出CD′:AP的值(不必写过程)

(1)求证:△BPO≌△PDE.
(2)当点P运动到OA的中点时,求出此时CD:AP的值.
(3)当点P运动到OC的中点时,满足题中条件的点D也随之在直线BC上运动到点D′,请画出此时的图形并直接写出CD′:AP的值(不必写过程)

考点:相似三角形的判定与性质,全等三角形的判定与性质
专题:
分析:(1)易证∠PBO=∠DPE和∠BOP=∠PED=90°,即可证明△BPO≌△PDE,即可解题;
(2)易证∠ABP=∠PBO,即可证明△ABP≌△CPD,根据全等三角形对应边相等可得AP=CD;
(3)作出图形,易证∠D'P'E=OBP',即可证明△BOP'≌△P'ED',可得P'E=OB,ED'=OP',即可求得
的值,即可解题.
(2)易证∠ABP=∠PBO,即可证明△ABP≌△CPD,根据全等三角形对应边相等可得AP=CD;
(3)作出图形,易证∠D'P'E=OBP',即可证明△BOP'≌△P'ED',可得P'E=OB,ED'=OP',即可求得
| AP′ |
| CD′ |
解答:证明:(1)∵PB=PD,
∴∠PDB=∠PBD,
∵AB=BC,∠ABC=90°,
∴∠C=45°,
∵BO⊥AC,
∴∠OBC=45°,
∴∠OBC=∠C=45°,
∵∠PBO=∠PBC-∠OBC,∠DPE=∠PDB-∠C,
∴∠PBO=∠DPE,
∵BO⊥AC,DE⊥AC,
∴∠BOP=∠PED=90°,
在△BPO和△PDE中,
,
∴△BPO≌△PDE(AAS);
(2)∵△ABP和△CPD,
∴∠ABP=∠PBO,
在△ABP和△CPD中,
,
∴△ABP≌△CPD(AAS),
∴AP=CD;
(3)作出图形,
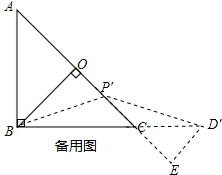
设∠OBP'=x,则∠P'BC=45°-x,
∵BP'=P'D',∴∠P'D'C=45°-x,
∵CD′=
D′E,D'E⊥CE,
∴∠CD'E=45°,CE=D'E,
∴∠P'D'E=90°-x,
∴∠D'P'E=OBP',
在△BOP'和△P'ED'中,
,
∴△BOP'≌△P'ED'(AAS),
∴P'E=OB,ED'=OP',
∵AP'=AO+OP'=3P'O,
CD'=
DE=
P'O,
∴
=
.
∴∠PDB=∠PBD,
∵AB=BC,∠ABC=90°,
∴∠C=45°,
∵BO⊥AC,
∴∠OBC=45°,
∴∠OBC=∠C=45°,
∵∠PBO=∠PBC-∠OBC,∠DPE=∠PDB-∠C,
∴∠PBO=∠DPE,
∵BO⊥AC,DE⊥AC,
∴∠BOP=∠PED=90°,
在△BPO和△PDE中,
|
∴△BPO≌△PDE(AAS);
(2)∵△ABP和△CPD,
∴∠ABP=∠PBO,
在△ABP和△CPD中,
|
∴△ABP≌△CPD(AAS),
∴AP=CD;
(3)作出图形,

设∠OBP'=x,则∠P'BC=45°-x,
∵BP'=P'D',∴∠P'D'C=45°-x,
∵CD′=
| 2 |
∴∠CD'E=45°,CE=D'E,
∴∠P'D'E=90°-x,
∴∠D'P'E=OBP',
在△BOP'和△P'ED'中,
|
∴△BOP'≌△P'ED'(AAS),
∴P'E=OB,ED'=OP',
∵AP'=AO+OP'=3P'O,
CD'=
| 2 |
| 2 |
∴
| AP′ |
| CD′ |
3
| ||
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△BPO≌△PDE、△ABP≌△CPD和△BOP'≌△P'ED'是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“十•一五”期间,安徽省各类项目验收补充耕地100余万亩,整理过的土地亩均增产约一成,新增粮食生产能力约1.6亿斤,1.6亿用科学记数法表示为( )
| A、1.6×108 |
| B、1.6×109 |
| C、16×107 |
| D、16×108 |
中国是仅次于美国的世界第二大经济体.国家统计局发布的《2013年国民经济和社会发展统计公报》显示2013年我国国内生产总值为56.89万亿元,同比增长7.7%,56.89万亿元用科学记数法表示为( )
| A、5.689×106亿元 |
| B、0.5689×106亿元 |
| C、5.689×105亿元 |
| D、5689×102亿元 |
 如图,在四边形ABCD中,E,F,M,N分别为AB,CD,BD,AC的中点,
如图,在四边形ABCD中,E,F,M,N分别为AB,CD,BD,AC的中点,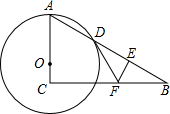 如图,已知点O是Rt△ABC的直角边AC上的一动点,以O为圆心,OA为半径的⊙O交AB于D点,DB垂直平分线交BC于F,交BD于E.
如图,已知点O是Rt△ABC的直角边AC上的一动点,以O为圆心,OA为半径的⊙O交AB于D点,DB垂直平分线交BC于F,交BD于E. 如图,以O为顶点的角有
如图,以O为顶点的角有 如图所示,∠BAF,∠CBD,∠ACE是△ABC的三个外角,求∠BAF+∠CBD+∠ACE的度数.
如图所示,∠BAF,∠CBD,∠ACE是△ABC的三个外角,求∠BAF+∠CBD+∠ACE的度数.