题目内容
在△ABC中，∠C=90°，点D在BC上，BD=4，AD=BC，tan∠ADC=| 4 |
| 3 |
（1）DC的长；
（2）sinB的值．
考点：解直角三角形
专题：
分析：（1）在Rt△ADC中，由tan∠ADC=
=
，可设AC=4k，则DC=3k，由勾股定理求出AD=5k，根据AD=BC列出方程5k=4+3k，求出k=2，于是DC=6；
（2）在Rt△ABC中，先利用勾股定理求出AB，再根据正弦函数的定义即可求出sinB的值．
| AC |
| DC |
| 4 |
| 3 |
（2）在Rt△ABC中，先利用勾股定理求出AB，再根据正弦函数的定义即可求出sinB的值．
解答：
解：（1）在Rt△ADC中，∵tan∠ADC=
=
，
∴可设AC=4k，则DC=3k，
由勾股定理，得AD=
=5k．
∵AD=BC，
∴5k=4+3k，
解得k=2，
∴DC=6；
（2）在Rt△ABC中，∵∠C=90°，
∴AB=
=
=2
，
∴sinB=
=
=
．
| AC |
| DC |
| 4 |
| 3 |
∴可设AC=4k，则DC=3k，
由勾股定理，得AD=
| AC2+DC2 |
∵AD=BC，
∴5k=4+3k，
解得k=2，
∴DC=6；
（2）在Rt△ABC中，∵∠C=90°，
∴AB=
| AC2+BC2 |
| 82+102 |
| 41 |
∴sinB=
| AC |
| AB |
| 8 | ||
2
|
4
| ||
| 41 |
点评：本题考查了解直角三角形，锐角三角函数的定义，勾股定理，难度中等，求出DC的值是解题的关键．
练习册系列答案
优学名师名题系列答案
相关题目
观察下列球的排列规律（其中●是实心球，
是空心球）：
从第一个球起到第2014个球止，共有实心球（ ）
是空心球）：从第一个球起到第2014个球止，共有实心球（ ）
| A、201个 | B、202个 |
| C、604个 | D、605个 |
对于分式
，永远成立的是（ ）
| 1 |
| x-1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，AD⊥DC，BC⊥DC，E是DC的一点，AE平分∠DAB．若反比例函数y=
图象在各个象限内y随着x的增大而增大，则m满足（ ）
| m+2 |
| x |
| A、m＜-2 | B、m＞-2 |
| C、m＜2 | D、m＞2 |
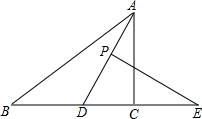在△ABC中，AD平分角∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E．