题目内容
 如图,AD⊥DC,BC⊥DC,E是DC的一点,AE平分∠DAB.
如图,AD⊥DC,BC⊥DC,E是DC的一点,AE平分∠DAB.(1)如果BE平分∠ABC,求证:点E是DC的中点;
(2)如果E是DC的中点,求证:BE平分∠ABC.
考点:角平分线的性质
专题:证明题
分析:(1)过点E作EF⊥AB于F,根据角平分线上的点到角的两边距离相等可得DE=EF,CE=EF,然后求出CE=DE,再根据线段中点的定义证明即可;
(2)根据角平分线上的点到角的两边距离相等可得DE=EF,根据线段中点的定义可得CE=DE,然后求出CE=EF,再根据到角的两边距离相等的点在角的平分线上证明.
(2)根据角平分线上的点到角的两边距离相等可得DE=EF,根据线段中点的定义可得CE=DE,然后求出CE=EF,再根据到角的两边距离相等的点在角的平分线上证明.
解答:
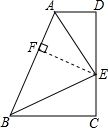 证明:(1)如图,过点E作EF⊥AB于F,
证明:(1)如图,过点E作EF⊥AB于F,
∵AD⊥DC,BC⊥DC,AE平分∠DAB,BE平分∠ABC,
∴DE=EF,CE=EF,
∴CE=DE,
∴点E是DC的中点;
(2)∵AD⊥DC,BC⊥DC,AE平分∠DAB,
∴DE=EF,
∵E是DC的中点,
∴CE=DE,
∴CE=EF,
∵EF⊥AB,BC⊥CD,
∴BE平分∠ABC.
 证明:(1)如图,过点E作EF⊥AB于F,
证明:(1)如图,过点E作EF⊥AB于F,∵AD⊥DC,BC⊥DC,AE平分∠DAB,BE平分∠ABC,
∴DE=EF,CE=EF,
∴CE=DE,
∴点E是DC的中点;
(2)∵AD⊥DC,BC⊥DC,AE平分∠DAB,
∴DE=EF,
∵E是DC的中点,
∴CE=DE,
∴CE=EF,
∵EF⊥AB,BC⊥CD,
∴BE平分∠ABC.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,到角的两边距离相等的点在角的平分线上,熟记两性质并作出辅助线是解题的关键.

练习册系列答案
相关题目
6m4n3÷(-3mn2)的结果为( )
| A、2m3n |
| B、-2m3n |
| C、-2m2n |
| D、m2n |
若p=x2y,则-x10y5•(-2x2y)3的计算结果是( )
| A、-8p8 |
| B、8p8 |
| C、-6p8 |
| D、6p8 |
抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中错误的是( )
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -37 | -21 | -9 | -1 | 3 | 3 | … |
| A、当x>1时y随x的增大而增大 | ||
B、抛物线的对称轴为x=
| ||
| C、当x=2时y=-1 | ||
| D、方程ax2+bx+c=0一个负数解x1满足-1<x1<0 |
下列选项中正确表示数轴的是( )
A、 |
B、 |
C、 |
D、 |
 如图,坐标平面有A(1,2),B(-2,1),C(0,-1),D(2,0)四个点,顺次连接A,B,C,D,求四边形ABCD的面积.
如图,坐标平面有A(1,2),B(-2,1),C(0,-1),D(2,0)四个点,顺次连接A,B,C,D,求四边形ABCD的面积. 在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,tan∠ADC=
在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,tan∠ADC=