题目内容
19.反比例函数y=$\frac{-2}{x}$的图象在第二、四象限,在每个象限内,y随x的增大而增大,反比例函数y=-$\frac{2}{x}$的图象在二、四象限,在它的图象上随增大而增大.分析 根据反比例函数y=$\frac{k}{x}$的系数k的符号来判断双曲线所在的象限以及函数图象的增减性.
解答 解:∵反比例函数y=$\frac{-2}{x}$中的-2<0,
∴该函数图象位于第二、四象限,且在每一象限内,y随x的增大而增大.
∵反比例函数y=-$\frac{2}{x}$中的-2<0,
∴该函数图象位于第二、四象限,且在每一象限内,y随x的增大而增大.
故答案是:二、四;增大;二、四;增大.
点评 本题考查了反比例函数的性质.对于反比例函数y=$\frac{k}{x}$,当k>0时,在每一个象限内,函数值y随自变量x的增大而减小;当k<0时,在每一个象限内,函数值y随自变量x增大而增大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.方程x2-3x=0的根是( )
| A. | x=3 | B. | x1=3,x2=-3 | C. | x1=$\sqrt{3}$,x2=-$\sqrt{3}$ | D. | x1=0,x2=3 |
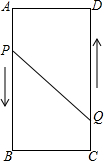 如图,四边形ABCD为矩形,AB=16cm.AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向B点移动,一直到达B点为止,点Q以2cm/s的速度向D点移动.
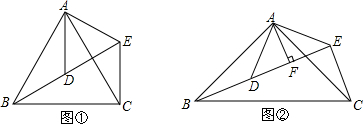
如图,四边形ABCD为矩形,AB=16cm.AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向B点移动,一直到达B点为止,点Q以2cm/s的速度向D点移动.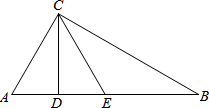 如图,CD是△ABC的AB边上的高,CE是AB边上的中线,且∠ACD=∠DCE=∠ECB,则∠B=30°.
如图,CD是△ABC的AB边上的高,CE是AB边上的中线,且∠ACD=∠DCE=∠ECB,则∠B=30°. 为了有效地利用土地,安徽省各大中城市兴建高楼,如图,小明在某高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,则该高楼的高度大约为( )
为了有效地利用土地,安徽省各大中城市兴建高楼,如图,小明在某高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,则该高楼的高度大约为( )