题目内容
10.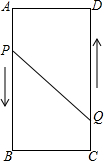 如图,四边形ABCD为矩形,AB=16cm.AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向B点移动,一直到达B点为止,点Q以2cm/s的速度向D点移动.
如图,四边形ABCD为矩形,AB=16cm.AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向B点移动,一直到达B点为止,点Q以2cm/s的速度向D点移动.(1)P、Q两点从出发开始到几秒时,四边形PBCQ的面积为33cm2?
(2)P、Q两点从出发开始到几秒时,点P和点Q之间的距离第一次是10cm?
(3)在运动过程中,点P和点Q之问的距离可能是18cm吗?如果可能,求出运动时间t,如果不可能,请说明理由.($\sqrt{2}$取1.4)
分析 (1)设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2,则PB=(16-3x)cm,QC=2xcm,根据梯形的面积公式可列方程:$\frac{1}{2}$(16-3x+2x)×6=33,解方程可得解;
(2)作QE⊥AB,垂足为E,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解;
(3)根据勾股定理得到矩形ABCD对角线的长,再与18cm比较大小即可作出判断.
解答 解:(1)设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2,
则PB=(16-3x)cm,QC=2xcm,
根据梯形的面积公式得$\frac{1}{2}$(16-3x+2x)×6=33,
解得x=5;
答: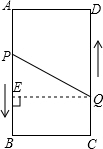 P、Q两点从出发开始到5秒时四边形PBCQ的面积为33cm2;
P、Q两点从出发开始到5秒时四边形PBCQ的面积为33cm2;
(2)设P,Q两点从出发经过t秒时,点P,Q间的距离是10cm,
作QE⊥AB,垂足为E,
则QE=AD=6,PQ=10,
∵PA=3t,CQ=BE=2t,
∴PE=AB-AP-BE=|16-5t|,
由勾股定理,得(16-5t)2+62=102,
解得t1=4.8(舍去),t2=1.6.
答:从出发到1.6秒时,点P和点Q的距离是10cm.
(3)∵$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{1{6}^{2}+{6}^{2}}$=$\sqrt{292}$<18,
∴在运动过程中,点P和点Q之问的距离不可能是18cm.
点评 考查了一元二次方程的应用,(1)主要用到了梯形的面积公式:S=$\frac{1}{2}$(上底+下底)×高;(2)作辅助线是关键,构成直角三角形后,用了勾股定理.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
15.在下列描述数据的方法中,( )反映数据的频数分布.
| A. | 扇形图 | B. | 条形图 | C. | 折线图 | D. | 直方图 |
20. 如图,△ABC中,∠A、∠B的角平分线相交于点D.若∠ADB=130°,则∠C等于( )
如图,△ABC中,∠A、∠B的角平分线相交于点D.若∠ADB=130°,则∠C等于( )
 如图,△ABC中,∠A、∠B的角平分线相交于点D.若∠ADB=130°,则∠C等于( )
如图,△ABC中,∠A、∠B的角平分线相交于点D.若∠ADB=130°,则∠C等于( )| A. | 80° | B. | 50° | C. | 40° | D. | 20° |