题目内容
5.同学们都知道,|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.试探索:(1)求|5-(-2)|=7.
(2)找出所有符合条件的整数x,使得|x+3|+|x-1|=4这样的整数是-3,-2,-1,0,1.
(3)由以上探索猜想对于任何有理数x,|x-3|+|x-5|是否有最小值?如果有写出最小值如果没有说明理由.
分析 (1)直接去括号,再按照去绝对值的方法去绝对值就可以了.
(2)要x的整数值可以进行分段计算,令x+3=0或x-1=0时,分为3段进行计算,最后确定x的值.
(3)根据(2)方法去绝对值,分为3种情况去绝对值符号,计算三种不同情况的值,最后讨论得出最小值.
解答 解:(1)原式=|5+2|=7.
故答案为:7;
(2)令x+3=0或x-1=0时,则x=-3或x=1.
当x<-3时,-(x+3)-(x-1)=4,
-x-3-x+1=4,解得x=-3(范围内不成立);
当-3≤x≤1时,(x+3)-(x-1)=4,
x+3-x+1=4,0x=0,x为任意数,
则整数x=-3,-2,-1,0,1;
当x>1时,(x+3)+(x-1)=4,
解得x=1(范围内不成立).
综上所述,符合条件的整数x有:-3,-2,-1,0,1.
故答案为-3,-2,-1,0,1;
(3)由(2)的探索猜想,对于任何有理数x,|x-3|+|x-5|有最小值为2.
点评 此题考查了整式的加减,去绝对值和数轴相联系的综合试题以及去绝对值的方法和去绝对值在数轴上的运用,难度较大,去绝对值的关键是确定绝对值里面的数的正负性.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14.-|$\frac{1}{2016}$|的倒数是( )
| A. | 2016 | B. | -2016 | C. | -$\frac{1}{2016}$ | D. | $\frac{1}{2016}$ |
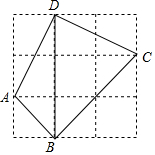 如图,在3×3的正方形网格中有一个四边形ABCD,若小正方形的边长为1,则sin∠ADB+cos∠DBC=$\frac{\sqrt{5}}{5}$+$\frac{\sqrt{2}}{2}$.
如图,在3×3的正方形网格中有一个四边形ABCD,若小正方形的边长为1,则sin∠ADB+cos∠DBC=$\frac{\sqrt{5}}{5}$+$\frac{\sqrt{2}}{2}$. 如图,△ACD≌△ECB,A、C、B在一条直线上,且A和E是一对对应顶点,如果∠BCE=130°,那么将△ACD绕着C点顺时针旋转50度与△ECB重合.
如图,△ACD≌△ECB,A、C、B在一条直线上,且A和E是一对对应顶点,如果∠BCE=130°,那么将△ACD绕着C点顺时针旋转50度与△ECB重合. 如图,∠B=40°,∠A=∠1-10°,∠ACD=65°,试说明AB∥CD.
如图,∠B=40°,∠A=∠1-10°,∠ACD=65°,试说明AB∥CD.