题目内容
9. 如图,正方形网格中的每个小正方形边长都是1,在如图的网格格点处取合适的A、B、C三点.AB=$\sqrt{5}$,BC=2$\sqrt{5}$,Ac=5.
如图,正方形网格中的每个小正方形边长都是1,在如图的网格格点处取合适的A、B、C三点.AB=$\sqrt{5}$,BC=2$\sqrt{5}$,Ac=5.(1)请在图中画出△ABC;
(2)∠ABC=90°;
(3)求点B到线段AC的距离.
分析 (1)在正方形网格中,根据勾股定理令AB=$\sqrt{5}$,BC=2$\sqrt{5}$,AC=5,从而画出△ABC;
(2)根据勾股定理的逆定理可得∠ABC的度数;
(3)利用三角形的面积公式,可求点B到线段AC的距离.
解答 解:(1)如图所示: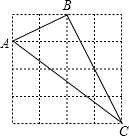
(2)∵AB=$\sqrt{5}$,BC=2$\sqrt{5}$,AC=5,
($\sqrt{5}$)2+(2$\sqrt{5}$)2=52,
∴△ABC是直角三角形,
∴∠ABC=90°.
故答案为:90°.
(3)$\sqrt{5}$×2$\sqrt{5}$÷2×2÷5
=5×2÷5
=2.
答:点B到线段AC的距离是2.
点评 考查了勾股定理、勾股定理的逆定理,直角三角形的面积.关键是熟练掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
相关题目
 如图,△ABC≌△ADC,若∠B=80°,∠BAC=35°,则∠BCD的度数为130度.
如图,△ABC≌△ADC,若∠B=80°,∠BAC=35°,则∠BCD的度数为130度. 如图是一个横断面为抛物线形状的拱桥,当水面宽8米时,拱顶(拱桥洞的最高点)离水面4m,水面上升1m时,水面的宽度为$4\sqrt{3}$.
如图是一个横断面为抛物线形状的拱桥,当水面宽8米时,拱顶(拱桥洞的最高点)离水面4m,水面上升1m时,水面的宽度为$4\sqrt{3}$. (1)用5块正方体的木块搭出如图所示的图形,画出它从正面、左面、上面三个方向看到的图形.
(1)用5块正方体的木块搭出如图所示的图形,画出它从正面、左面、上面三个方向看到的图形. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的方程ax2+bx+c=0的根是x1=0,x2=2;关于x的方程ax2+bx+c-2=0的根是x=1.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的方程ax2+bx+c=0的根是x1=0,x2=2;关于x的方程ax2+bx+c-2=0的根是x=1.