题目内容
17.证明:等腰三角形两腰上的高相等(画图,写已知、求证并证明).分析 根据已知画出图形,易证△ACE≌△ABD,根据全等三角形的性质,得CE=BD.
解答 解:已知:AB=AC,CE⊥AB于E,BD⊥AC于D.
求证:BD=CE.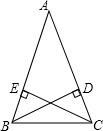
证明:∵AB=AC,CE⊥AB于E,BD⊥AC于D,
∴∠AEC=∠ADB=90°,
在△ACE和△ABD中,
$\left\{\begin{array}{l}{∠A=∠A}\\{∠AEC=∠ADB}\\{AC=AB}\end{array}\right.$,
∴△ACE≌△ABD,
∴CE=BD.
点评 本题考查了全等三角形的判定与性质及等腰三角形的性质;证明的步骤是:先根据题意画出图形,再根据图形写出已知和求证,最后写出证明过程.

练习册系列答案
相关题目
7.将抛物线y=(x-1)2+2向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的顶点坐标为( )
| A. | (1,4) | B. | (4,4) | C. | (-2,6) | D. | (4,6) |
8. 把一个半圆对折两次(如图),折痕OA与OB的夹角为( )
把一个半圆对折两次(如图),折痕OA与OB的夹角为( )
 把一个半圆对折两次(如图),折痕OA与OB的夹角为( )
把一个半圆对折两次(如图),折痕OA与OB的夹角为( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
 如图,C是AB的中点,∠A=∠B,∠BCD=∠ACE,求证:AD=BE.
如图,C是AB的中点,∠A=∠B,∠BCD=∠ACE,求证:AD=BE.
 一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-$\frac{8}{x}$的图象交于A(-2,b)、B两点.若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,则m的值为( )
一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-$\frac{8}{x}$的图象交于A(-2,b)、B两点.若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,则m的值为( ) 如图,正方形网格中的每个小正方形边长都是1,在如图的网格格点处取合适的A、B、C三点.AB=$\sqrt{5}$,BC=2$\sqrt{5}$,Ac=5.
如图,正方形网格中的每个小正方形边长都是1,在如图的网格格点处取合适的A、B、C三点.AB=$\sqrt{5}$,BC=2$\sqrt{5}$,Ac=5. 将边长相等的正方形、正六边形的一边重合丙叠在一起,过正六边形的顶点B作正方形的边AC的垂线,垂足为点D,则tan∠ABD=2-$\sqrt{3}$.
将边长相等的正方形、正六边形的一边重合丙叠在一起,过正六边形的顶点B作正方形的边AC的垂线,垂足为点D,则tan∠ABD=2-$\sqrt{3}$.