题目内容
17.已知函数y=(m-1)x2+x-m+2(m为常数).(1)求证:不论m为何值,该函数的图象与x轴总有交点;
(2)当m为何值时,函数图象过原点,并指出此时函数图象与x轴的另一个交点;
(3)在(2)的情况下,怎样平移使得顶点落在x轴上,直接写出平移前后图象、对称轴和y轴围成的图形的面积.
分析 (1)分类讨论m=1或m≠1时,函数图象与x轴的交点情况;
(2)根据函数y=(m-1)x2+x-m+2过原点求出m的值,进而求出函数图象与x轴的另一个交点;
(3)首先求出函数y=x2+x的顶点坐标,然后结合平移知识即可求出平移前后图象、对称轴和y轴围成的图形的面积.
解答 (1)证明:∵若m=1时,函数为一次函数,与x轴有交点,
若m≠1时,函数为二次函数,y=(m-1)x2+x-m+2
△=1-4(m-1)(2-m)=(2m-3)2≥0,
∴不论m为何值,该函数的图象与x轴总有交点;
(2)解:∵函数y=(m-1)x2+x-m+2过原点,
∴-m+2=0,
∴m=2,
∴y=x2+x,
令y=x2+x=0,
解得x=0或x=-1,
∴函数图象与x轴的另一个交点为(-1,0);
(3)解:∵y=x2+x,
∴y=(x+$\frac{1}{2}$)2-$\frac{1}{4}$,
∴顶点为$(-\frac{1}{2},-\frac{1}{4})$,
∴函数的图象向上平移$\frac{1}{4}$个单位顶点落在x轴上,
围成部分面积利用平移转化成平行四边形PQMN,面积为$\frac{1}{2}$×$\frac{1}{4}$=$\frac{1}{8}$.
点评 本题主要考查了抛物线与x轴交点以及二次函数图象的平移的知识,解答本题的关键是熟练掌握二次函数的性质以及割补法求不规则图形的面积,此题难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一次中学生田径运动会上,参加男子跳高的20名运动员成绩如下所示:
则下列叙述正确的是( )
| 成绩(单位:米) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
| 人数 | 2 | 3 | 2 | 4 | 5 | 2 | 1 | 1 |
| A. | 这些运动员成绩的中位数是1.70 | B. | 这些运动员成绩的众数是5 | ||
| C. | 这些运动员的平均成绩是1.71875 | D. | 这些运动员成绩的方差是0.0725 |
5.$\frac{{\sqrt{5}}}{2}$是( )
| A. | 分数 | B. | 有理数 | C. | 小数 | D. | 整数 |
9.下面四个汽车标志图案中,是中心对称而不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图是由几个相同的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,则这个几何体的左视图是( )
如图是由几个相同的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,则这个几何体的左视图是( )



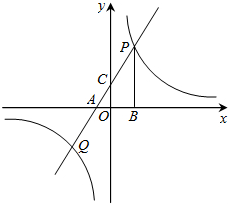 如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=$\frac{3}{2}$,点B的坐标为(4,0).
如图,经过点A(-2,0)的一次函数y=ax+b(a≠0)与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=$\frac{3}{2}$,点B的坐标为(4,0).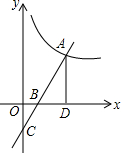 如图,直线y=2x-4与反比例函数y=$\frac{k}{x}$的图象交于第一象限的点A,与x轴、y轴分别交于点B,C,AD⊥x轴于点D.如果△BOC与△BDA的面积之比等于4:9,则k=30.
如图,直线y=2x-4与反比例函数y=$\frac{k}{x}$的图象交于第一象限的点A,与x轴、y轴分别交于点B,C,AD⊥x轴于点D.如果△BOC与△BDA的面积之比等于4:9,则k=30.