题目内容
12.已知抛物线y=x2-2x-3的顶点为D,点P、Q是抛物线上的动点,若△DPQ是等边三角形,求△DPQ的边长.分析 y=x2-2x-3可变形为y=(x-1)2-4,从而求得点D的坐标;根据题意设P点坐标为(1+k,-4+$\sqrt{3}$k),然后利用二次函数图象上坐标的特征求得关于k的一元二次方程,解方程即可求得k的值,进而求得△DPQ的边长.
解答 解:y=x2-2x-3可变形为y=(x-1)2-4,
∴D点坐标为(1,-4),
要使△DPQ是等边三角形,则PQ∥x轴,
∴设P点坐标为(1+k,-4+$\sqrt{3}$k),
∴-4+$\sqrt{3}$k=(1+k)2-2×(1+k)-3,
解得:k1=0(舍去),k2=$\sqrt{3}$,PQ=2k=2$\sqrt{3}$,
∴△DPQ的边长为2$\sqrt{3}$.
点评 本题考查了二次函数的性质、二次函数图象上点的坐标特征、等边三角形的性质.根据二次函数的性质和等边三角形的性质得出PQ∥x轴是解题的关键.

练习册系列答案
相关题目
1.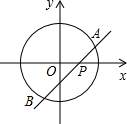 如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
 如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )| A. | -2≤x≤2 | B. | -2$\sqrt{2}$<x<2$\sqrt{2}$ | C. | 0≤x≤2$\sqrt{2}$ | D. | -2$\sqrt{2}$≤x≤2$\sqrt{2}$ |
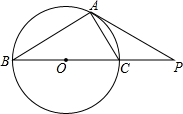 如图,P是⊙O外一点,PA切⊙O于点A,直线PO交⊙O于B,C两点.已知PC=2,AP=2$\sqrt{3}$.求:
如图,P是⊙O外一点,PA切⊙O于点A,直线PO交⊙O于B,C两点.已知PC=2,AP=2$\sqrt{3}$.求: 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AC于E,EF⊥BC于F.求证:EF:DF=BC:AC.
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AC于E,EF⊥BC于F.求证:EF:DF=BC:AC.