题目内容
二次函数y=（x-a）（x-b）-1与x轴的交点坐标为（m，0），（n，0），且a＜b，m＜n．则实数a，b，m，n的大小关系是（ ）
| A、m＜a＜b＜n |
| B、a＜m＜b＜n |
| C、a＜b＜m＜n |
| D、a＜m＜n＜b |
考点：抛物线与x轴的交点
专题：
分析：根据交点式可以画出y′=（x-a）（x-b）的大致图象，根据平移从而确定y=（x-a）（x-b）-1图象，利用图象就可以求出答案．
解答：解：设y′=（x-a）（x-b）的大致图象如图所示，抛物线①，它与x轴的交点坐标的横坐标依次为a、b，
∴y=（x-a）（x-b）-1由抛物线①向下平移1单位长度得到的．如图中的抛物线②，它与x轴的交点横坐标分别是m、n，
有∵a＜b，m＜n，
∴图象得m＜a＜b＜n，
故选A．
∴y=（x-a）（x-b）-1由抛物线①向下平移1单位长度得到的．如图中的抛物线②，它与x轴的交点横坐标分别是m、n，
有∵a＜b，m＜n，
∴图象得m＜a＜b＜n，
故选A．
点评：：本题是一道二次函数的综合试题，考查了二次函数的图象性质，二次函数图象的平移及二次函数的图象与x轴的交点坐标的特征．
练习册系列答案
相关题目
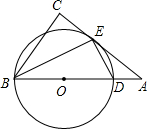如图，Rt△ABC中，∠C=90°，∠B的平分线交AC于E，DE⊥BE．
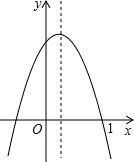已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，抛物线经过点（1，0），则下列结论：