题目内容
7.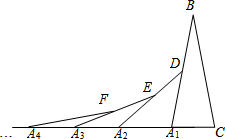 如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第5个等腰三角形的底角度数是5°.
如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第5个等腰三角形的底角度数是5°.
分析 先根据等腰三角形的性质求出∠BA1C的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠DA2A1,∠EA3A2及∠FA4A3的度数,找出规律即可得出第n个等腰三角形的底角度数.
解答 解:∵在△CBA1中,∠B=20°,A1B=CB,
∴∠BA1C=$\frac{180°-∠B}{2}$=80°,
∵A1A2=A1D,∠BA1C是△A1A2D的外角,
∴∠DA2A1=$\frac{1}{2}$∠BA1C=$\frac{1}{2}$×80°;
同理可得,
∠EA3A2=($\frac{1}{2}$)2×80°,∠FA4A3=($\frac{1}{2}$)3×80°,
∴第n个等腰三角形的底角度数是($\frac{1}{2}$)n-1×80°.
∴第5个等腰三角形的底角度数为:$(\frac{1}{2})^{4}×80°$=5°,
故答案为:5°.
点评 本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠DA2A1,∠EA3A2及∠FA4A3的度数,找出规律是解答此题的关键.

练习册系列答案
相关题目
12.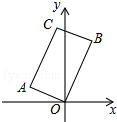 如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
 如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{7}{4}$,$\frac{7}{2}$)、(-$\frac{1}{2}$,4) | B. | ($\frac{3}{2}$,3)、(-$\frac{2}{3}$,4) | C. | ($\frac{3}{2}$,3)、(-$\frac{1}{2}$,4) | D. | ($\frac{7}{4}$,$\frac{7}{2}$)、(-$\frac{2}{3}$,4) |
16.表示两个变量之间的关系,下列说法错误的是( )
| A. | 用表格可以表示任意两个变量之间的关系 | |
| B. | 用关系式可以表示任意两个变量之间的关系 | |
| C. | 用图象可以表示任意两个变量之间的关系 | |
| D. | 在某一变化过程中,数值始终不变的量叫常量 |

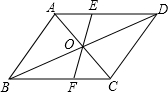 如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=4,BC=6,OE=2,那么四边形EFCD周长是( )
如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=4,BC=6,OE=2,那么四边形EFCD周长是( ) 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.