题目内容
17. 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.求证:△ACD≌△CBE.
分析 根据垂直的定义可得∠ADC=∠E=90°,然后根据同角的余角相等求出∠B=∠ACD,再利用“角角边”证明△ACD≌△CBE.
解答 证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∵∠B+∠BCE=90°,
∴∠B=∠ACD,
在△BEC和△CDA中,$\left\{\begin{array}{l}{∠ADC=∠E}\\{∠ACD=∠B}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△CBE(AAS).
点评 本题考查了全等三角形的判定与性质,根据题意求出∠B=∠ACD是证明三角形全等的关键.

练习册系列答案
相关题目
8.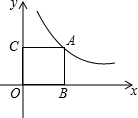 如图,点A是反比例函数y=$\frac{k}{x}(x>0)$图象上一点,AB垂直于x轴,垂足为点B,AC垂直于y轴,垂足为点C,若矩形ABOC的面积为5,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}(x>0)$图象上一点,AB垂直于x轴,垂足为点B,AC垂直于y轴,垂足为点C,若矩形ABOC的面积为5,则k的值为( )
 如图,点A是反比例函数y=$\frac{k}{x}(x>0)$图象上一点,AB垂直于x轴,垂足为点B,AC垂直于y轴,垂足为点C,若矩形ABOC的面积为5,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}(x>0)$图象上一点,AB垂直于x轴,垂足为点B,AC垂直于y轴,垂足为点C,若矩形ABOC的面积为5,则k的值为( )| A. | 5 | B. | 2.5 | C. | $\sqrt{5}$ | D. | 10 |
5.下列算式中,与-1+2相等的是( )
| A. | 2-1 | B. | -1-2 | C. | -(2-1) | D. | -(1+2) |
12.无论m为何值,点A(m,5-2m)不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.下列运算正确的是( )
| A. | a2•a4=a8 | B. | 2a+3a=5a | C. | (x-2)2=x2-4 | D. | (x-2)(x+3)=x2-6 |
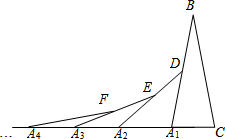 如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第5个等腰三角形的底角度数是5°.
如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第5个等腰三角形的底角度数是5°.