题目内容
13.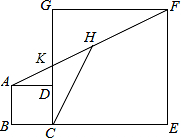 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,连结AF交CG于点K,H是AF的中点,连结CH.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,连结AF交CG于点K,H是AF的中点,连结CH.(1)求tan∠GFK的值;
(2)求CH的长.
分析 (1)由正方形的性质得出AD=CD=BC=1,CG=FG=CE=3,AD∥BC,GF∥BE,∠G=90°,证出△ADK∽△FGK,得出比例式求出GK=$\frac{3}{4}$DG=$\frac{3}{2}$,即可得出结果;
(2)由正方形的性质求出AB=BC=1,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=$\frac{1}{2}$AF,根据勾股定理求出AF,即可得出结果.
解答 解:(1)∵四边形ABCD和四边形CEFG是正方形,
∴AD=CD=BC=1,CG=FG=CE=3,AD∥BC,GF∥BE,∠G=90°,
∴DG=CG-CD=2,AD∥GF,
∴△ADK∽△FGK,
∴DK:GK=AD:GF=1:3,
∴GK=$\frac{3}{4}$DG=$\frac{3}{2}$,
∴tan∠GFK=$\frac{GK}{FG}$=$\frac{\frac{3}{2}}{3}$=$\frac{1}{2}$;
(2)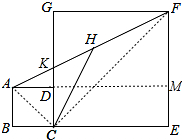 ∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
延长AD交EF于M,连接AC、CF,如图所示:
则AM=BC+CE=1+3=4,FM=EF-AB=3-1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
∵H为AF的中点,
∴CH=$\frac{1}{2}$AF,
在Rt△AMF中,由勾股定理得:AF=$\sqrt{A{M}^{2}+F{M}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴CH=$\frac{1}{2}$AF=$\sqrt{5}$.
点评 本题考查了相似三角形的判定与性质、三角函数、勾股定理,正方形的性质,直角三角形斜边上的中线性质;本题有一定难度,特别是(2)中,需要通过作出辅助线运用直角三角形斜边上的中线性质才能得出结果.

 名校课堂系列答案
名校课堂系列答案| A. | $\root{3}{-27}$ | B. | ($\sqrt{2}$-1)0 | C. | $\sqrt{12}$ | D. | $\sqrt{(-2{)^2}}$ |
| 成本P(元/千克) | 8-$\frac{x}{10}$ |
| 采摘量q(千克) | 1000-10x |
(2)该养殖葡萄户,每天获得的利润为y(元),y关于x的关系是什么?第几天利润最大;
(3)该养殖葡萄户决定,每销售1千克捐养老院m(m≤2)元,满足每天获得的利润随x的增大而增大,求m的取值范围.
| A. | a2+a3=a5 | B. | (a3)2=a5 | C. | (a+3)2=a2+9 | D. | -2a2•a=-2a3 |
| A. | a2+b2 | B. | a2-a+2 | C. | a2+3b | D. | (x+y)2-4 |