题目内容
10.计算:$\sqrt{\frac{1}{100}}$-(-2)3×$\root{3}{0.064}$+$\sqrt{5}$($\sqrt{5}$-$\frac{2}{\sqrt{5}}$)分析 本题涉及算术平方根、立方、开立方、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:$\sqrt{\frac{1}{100}}$-(-2)3×$\root{3}{0.064}$+$\sqrt{5}$($\sqrt{5}$-$\frac{2}{\sqrt{5}}$)
=0.1+8×0.4+5-2
=0.1+3.2+5-2
=6.3.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握算术平方根、立方、开立方、二次根式等考点的运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.要清楚地表示出个部分在总体积中所占的百分比,应选择( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 上述3种都可以 |
15.若x>y,则下列式子错误的是( )
| A. | 3-x>3-y | B. | x-3>y-3 | C. | x+3>y+2 | D. | $\frac{x}{3}$>$\frac{y}{3}$ |
2.某特警对为了选拔“神枪手”举行射击比赛,最后由甲、乙两名战士进入决赛,两人各射靶10次,经过统计计算,甲、乙两名战士的总成绩都是99.68环,甲的方差是0.28,乙的方差是0.21,则下列说法中,正确的是( )
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩稳定 | ||
| C. | 甲、乙两人成绩的稳定性相同 | D. | 无法确定谁的成绩更稳定 |
19.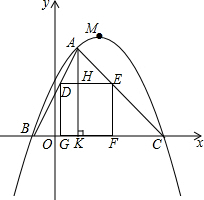 如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
(1)求出这条抛物线的解析式;
(2)求正方形DEFG的边长;
(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP的周长最小?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
 如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:| x | … | -2 | 0 | 4 | 8 | 10 | … |
| y | … | 0 | 5 | 9 | 5 | 0 | … |
(2)求正方形DEFG的边长;
(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP的周长最小?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
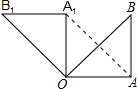 如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=5,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=5,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.