题目内容
8.(1)32+(-2-5)÷7-|-$\frac{1}{4}$|×(-2)2.(2)25×$\frac{3}{4}$-(-25)×$\frac{1}{2}$+25×(-$\frac{1}{4}$)
(3)-14-(1-0.5)×$\frac{1}{3}$×[10-(-2)2]-(-1)3.
(4)-9÷3+($\frac{1}{2}$-$\frac{2}{3}$)×12+32.
分析 (1)先算括号里面的,再算乘方,乘法,最后算加减即可
(2)逆用乘法分配律进行计算即可;
(3)、(4)先算括号里面的,再算乘方,乘法,最后算加减即可.
解答 解:(1)原式=9-7÷7-$\frac{1}{4}$×4
=9-1-1
=7;
(2)原式=25×$\frac{3}{4}$+25×$\frac{1}{2}$-25×$\frac{1}{4}$
=25×($\frac{3}{4}$+$\frac{1}{2}$-$\frac{1}{4}$)
=25×1
=25;
(3)原式=-1-0.5×$\frac{1}{3}$×(10-4)+1
=-1-$\frac{1}{6}$×6+1
=-1-1+1
=-1;
(4)原式=-9÷3+(-$\frac{1}{6}$)×12+9
=-9÷3-2+9
=-3-2+9
=4.
点评 本题考查的是有理数的混合运算,熟知有理数混合运算的顺序是解答此题的关键.

练习册系列答案
相关题目
18.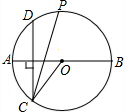 如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )
如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )
 如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )
如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )| A. | 到CD的距离保持不变 | B. | 到D点距离保持不变 | ||
| C. | 等分$\widehat{BD}$ | D. | 位置不变 |
19.代数式-7,x,-m,x2y,$\frac{x+y}{2}$,-5ab2c3,$\frac{1}{y}$中,单项式有5个,其中系数为1的有x,x2y,系数为-1的有-m,次数是1的有x,-m,.
3.已知点M(a,3),B(2,b)关于x轴对称,则a+b的值( )
| A. | -5 | B. | 5 | C. | -1 | D. | 1 |
17.下列说法中,正确的是( )
| A. | 希望小学初一年级的367名同学中,至少有两个生日相同的概率是1 | |
| B. | 在投掷骰子时,连投两次点数相同的概率与连投两次点数都为1的概率相等 | |
| C. | 我们小组共8名同学,他们中肯定有两人在同一月过生日 | |
| D. | 一个游戏的中奖率是1%,买100张奖券,一定会中奖 |
18.长方形的周长为c米,宽为x米,则长为( )
| A. | (c-2x)米 | B. | $\frac{c-2x}{2}$米 | C. | $\frac{c-x}{2}$米 | D. | $\frac{c}{2}$-2x米 |