题目内容
14.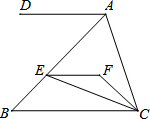 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=130°,∠FEC=15°,求∠ACF的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=130°,∠FEC=15°,求∠ACF的度数.
分析 先根据平行线的性质得出∠ACB的度数,再由EF∥AD,AD∥BC得出EF∥BC,故∠BCE=∠FEC,根据角平分线的性质得出∠BCF=2∠BCE,由∠ACF=∠ACB-∠BCF即可得出结论.
解答 解:∵AD∥BC,
∴∠ACB+∠DAC=180°.
∵∠DAC=130°,
∴∠ACB=50°.
∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠BCE=∠FEC=15°.
又∵CE平分∠BCF,
∴∠BCF=2∠BCE=30°,
∴∠ACF=∠ACB-∠BCF=20°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等,同旁内角互补.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列命题中,是真命题的是( )
| A. | 平分弦的直径垂直于弦 | B. | 相等圆周角所对的弧相等 | ||
| C. | 任意三个点确定一个圆 | D. | 圆内接平行四边形必为矩形 |
19.2015年,菏泽市相关部门统计,春节一周长假期间共实现销售收入约3.284亿元,比同期增长4.8%,请你将3.284亿用科学记数法表示为( )
| A. | 3.284×108 | B. | 32.84×107 | C. | 3.284×107 | D. | 32.84×108 |
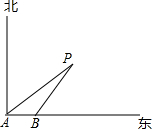 如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,$\sqrt{3}$≈1.73)
如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,$\sqrt{3}$≈1.73)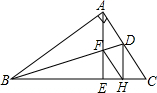 已知,如图,在Rt△ABC中,∠A=90°,AE是高,BD是∠ABC的平分线,AE与BD相交于点F,DH⊥BC,垂足为H,求证:四边形AFHD是菱形.
已知,如图,在Rt△ABC中,∠A=90°,AE是高,BD是∠ABC的平分线,AE与BD相交于点F,DH⊥BC,垂足为H,求证:四边形AFHD是菱形.