题目内容
18. 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长为18.
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=6,AD=8,则四边形ABOM的周长为18.
分析 根据矩形的性质,直角三角形斜边中线性质,三角形中位线性质求出BO、OM、AM即可解决问题.
解答 解: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴AD=BC=8,AB=CD=6,∠ABC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∵AO=OC,
∴BO=$\frac{1}{2}$AC=5,
∵AO=OC,AM=MD=4,
∴OM=$\frac{1}{2}$CD=3,
∴四边形ABOM的周长为AB+OB+OM+AM=6+5+3+4=18.
故答案为18.
点评 本题看成矩形的性质、三角形中位线定理、直角三角形斜边中线性质等知识,解题的关键是灵活应用中线知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
6.有三张背面完全相同、正面分别写有整数-1,1,2的卡片,现将这三张卡片背面朝上洗匀随机抽取一张,正面的数记为m,再从剩余的两张卡片中随机抽取一张,其正面上的数记为n,则m•n的值是负数的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
13.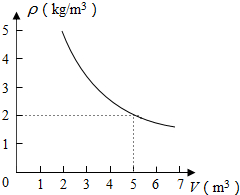 在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是( )
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是( )
 在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是( )
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是( )| A. | 1kg/m3 | B. | 2kg/m3 | C. | 100kg/m3 | D. | 5kg/m3 |
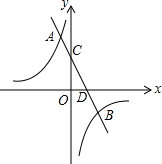 如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-1,6)和点B(3,m),与y轴交于点C,与x轴交于点D.
如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-1,6)和点B(3,m),与y轴交于点C,与x轴交于点D.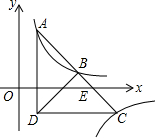 如图,Rt△ADC在平面直角坐标系下如图放置,斜边AC交x轴于点E,过点A的双曲线y=$\frac{k}{x}$(m≠0)交Rt△ADC斜边AC的中点B,连接BD,过点C作双曲线y=$\frac{m}{x}$(m≠0).若BD=3BE,A的坐标为(1,8),则m=( )
如图,Rt△ADC在平面直角坐标系下如图放置,斜边AC交x轴于点E,过点A的双曲线y=$\frac{k}{x}$(m≠0)交Rt△ADC斜边AC的中点B,连接BD,过点C作双曲线y=$\frac{m}{x}$(m≠0).若BD=3BE,A的坐标为(1,8),则m=( )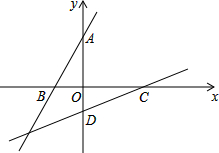 已知A、B、C、D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的表达式为y1=k1x+b1,直线CD的表达式为y2=k2x+b2,则k1•k2=1.
已知A、B、C、D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的表达式为y1=k1x+b1,直线CD的表达式为y2=k2x+b2,则k1•k2=1.