题目内容
2.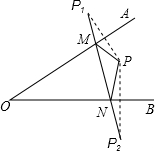 如图,∠AOB=30°,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,OP=18,图中线段之间相等的关系式有(至少写出两组)PM=P1M,PN=P2N;△PMN的周长为18.
如图,∠AOB=30°,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,OP=18,图中线段之间相等的关系式有(至少写出两组)PM=P1M,PN=P2N;△PMN的周长为18.
分析 根据轴对称的性质可得PM=P1M,PN=P2N,连接OP、OP1、OP2,根据轴对称的性质可得OP=OP1=OP2,∠POM=∠P1OM,∠PON=∠P1ON,然后求出△P1OP2是等边三角形,根据等边三角形的性质可得P1P2=OP1,再求出△PMN的周长=P1P2,从而得解.
解答 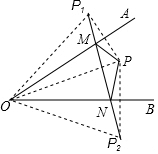 解:∵P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,
解:∵P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,
∴PM=P1M,PN=P2N,
如图,连接OP、OP1、OP2,
∵P点关于OA、OB的对称点P1,P2,
∴OP=OP1=OP2=18,
∠POM=∠P1OM,∠PON=∠P1ON,
∵∠AOB=30°,
∴∠P1OP2=2∠AOB=2×30°=60°,
∴△P1OP2是等边三角形,
∴P1P2=OP1=18,
△PMN的周长=PM+MN+PN=P1M+MN+P2N=P1P2=18.
故答案为:PM=P1M,PN=P2N;18.
点评 本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若点A(-3,y)在第三象限,则点B(-3,-y)在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
14.若m≠0,n≠0,m>n,化简二次根式$\sqrt{-{m}^{3}n}$的结果是( )
| A. | -m$\sqrt{-mn}$ | B. | -m$\sqrt{mn}$ | C. | m$\sqrt{mn}$ | D. | m$\sqrt{-mn}$ |
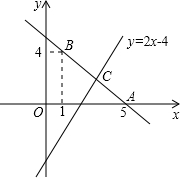 已知直线y=kx+b经过点A(5,0),B(1,4).
已知直线y=kx+b经过点A(5,0),B(1,4).