题目内容
8.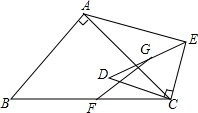 如图,△ABC和△CDE均为等腰直角三角形,∠BAC=∠DCE=90°,且AC=2CE,F、G分别为BC、DE边上的中点,连接AE、FG,AE=3,则FG的长度为( )
如图,△ABC和△CDE均为等腰直角三角形,∠BAC=∠DCE=90°,且AC=2CE,F、G分别为BC、DE边上的中点,连接AE、FG,AE=3,则FG的长度为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{3\sqrt{2}}{2}$ |
分析 由△ABC和△CDE均为等腰直角三角形△ABC是等腰直角三角形,F、G分别为BC、DE边上的中点,得到∠ACF=∠ECG=45°,CF=$\frac{\sqrt{3}}{2}$AC,CG=$\frac{\sqrt{2}}{2}$CE,证得∠FCG=∠ACE,$\frac{CF}{HC}=\frac{CG}{CE}\frac{\sqrt{2}}{2}$,推出△FCG~△ACE,即可得到结果.
解答 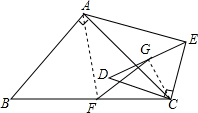 解:连接AF,CG,
解:连接AF,CG,
∵△ABC是等腰直角三角形,点F是BC边上的中点,
∴∠ACF=45°,CF=$\frac{\sqrt{3}}{2}$AC,
∵△CDE为等腰直角三角形,点G是BC边上的中点,
∴∠ECG=45°
CG=$\frac{\sqrt{2}}{2}$CE,
∴∠ACF=∠ECG,
∴∠ACF+∠ACG=∠ECG+∠ACG.
∴∠FCG=∠ACE,
∵$\frac{CF}{HC}$=$\frac{CG}{CE}$=$\frac{\sqrt{2}}{2}$,
∴△FCG~△ACE,
∴$\frac{FG}{AE}$=$\frac{\sqrt{2}}{2}$,
∵AE=3,
∴FG=$\frac{3\sqrt{2}}{2}$.
故选D.
点评 本题考查了等腰直角三角形的性质,相似三角形的判定和性质,熟记相似三角形的判定定理是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
2.某校准备修建一个面积为180平方米的矩形活动场地,它的长比宽多11米,设场地的宽为x米,则可列方程为( )
| A. | x(x-11)=180 | B. | 2x+2(x-11)=180 | C. | x(x+11)=180 | D. | 2x+2(x+11)=180 |
20.一元二次方程x2+4x-3=0的两根为x1、x2,则x1•x2的值是( )
| A. | 4 | B. | -4 | C. | 3 | D. | -3 |
3.下列各式中,计算正确的是( )
| A. | (3x-y)(3x-y)=9x2-y2 | B. | (-x+y)(-x-y)=x2-y2 | C. | (x+9)(x-9)=x2-9 | D. | (x-1)2=x2-2x-1 |
18.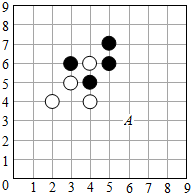 甲乙两位同学用围棋子做游戏.如图所示.现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也组成轴对称图形.则下列下子方法不正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )
甲乙两位同学用围棋子做游戏.如图所示.现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也组成轴对称图形.则下列下子方法不正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )
 甲乙两位同学用围棋子做游戏.如图所示.现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也组成轴对称图形.则下列下子方法不正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )
甲乙两位同学用围棋子做游戏.如图所示.现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也组成轴对称图形.则下列下子方法不正确的是[说明:棋子的位置用数对表示,如A点在(6,3)]( )| A. | 黑(3,7);白(3,5) | B. | 黑(4,7);白(6,2) | C. | 黑(3,7);白(5,3) | D. | 黑(4,7);白(2,6) |
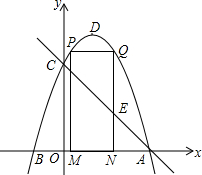 如图,直线y=-x+3与x轴、y轴分别交于A、C两点,对称轴为直线x=1的抛物线过A、C两点,抛物线与x轴的另一个交点为点B(B在A的左侧),顶点为D.
如图,直线y=-x+3与x轴、y轴分别交于A、C两点,对称轴为直线x=1的抛物线过A、C两点,抛物线与x轴的另一个交点为点B(B在A的左侧),顶点为D.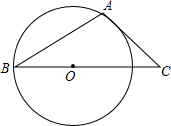 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C的大小等于40.
如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C的大小等于40.