题目内容
11.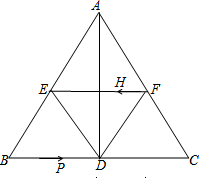 如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
分析 (1)根据等腰三角形的性质,证得点D是BC的中点;根据三角形的中位线定理,即可证得:DE∥AC,DF∥AB,根据题目中的条件,即可证得结论;
(2)根据中位线定理,即可求出线段EF的长度;根据菱形的面积等于对角线乘积的一半,即可求出菱形面积;
(3)根据平行四边形的对边相等,列出关于t的方程,求出t即可.
解答 (1)证明:∵AB=AC,AD⊥BC,
∴D为BC的中点,
∵E,F分别为AB,AC的中点,
∴DE和DF是△ABC的中位线,
∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵E,F分别为AB,AC的中点,AB=AC,
∴AE=AF∴平行四边形AEDF是菱形;
(2)解:∵EF为△ABC的中位线,
∴EF=$\frac{1}{2}$BC=5,
∵AD=8,AD⊥EF,
∴S菱形AEDF=$\frac{1}{2}$AD•EF=$\frac{1}{2}$×8×5=20;
(3)解:∵EF∥BC
∴EH∥BP,
若四边形BPHE为平行四边形,则需EH=BP,
∴5-2t=3t,解得:t=1,
∴当t=1秒时,四边形BPHE为平行四边形,
∵EF∥BC,
∴FH∥PC,
若四边形PCFH为平行四边形,则需FH=PC,
∴2t=10-3t,解得:t=2,
∴当t=2秒时,四边形PCFH为平行四边形.
点评 本题主要考查了等腰三角形的性质、菱形的性质与判定、平行四边形的性质与判定的综合应用,解决此类问题,需要将各知识点融合,熟练应用相关的知识点是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
16.平面直角坐标系中,若平移二次函数y=(x-2010)(x-2011)+4的图象,使其与x轴交于两点,且此两点的距离为1个单位,则平移方式为( )
| A. | 向左平移4个单位 | B. | 向右平移4个单位 | C. | 向上平移4个单位 | D. | 向下平移4个单位 |
 画出如图组合体的三种视图.
画出如图组合体的三种视图. 已知:如图,△ABC中.
已知:如图,△ABC中.