题目内容
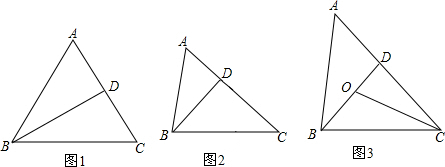
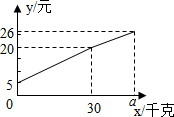
7.数学活动:数学活动课上,老师提出如下数学问题:已知四边形ABCD与BEFG都为正方形,P为DF的中点,连接AP,EP,如图1,当点F与点C重合时,求证:AP=PE,AP⊥PE.
独立思考:请你证明老师提出的问题;
合作交流:解决完上述问题后,“翱翔”小组的同学受此启发,把正方形BEFG绕点B逆时针旋转,当F落在BD上时(如图2),他们认为老师提出的结论仍然成立.
“翱翔”小组的认识是否正确?请说明理由.
发现问题:解决完上述问题后,如图(3),老师将正方形BEFG在图1的基础上绕点B旋转角度α(0°<α<360°),让同学们写出有关△APE的正确结论.“兴趣”小组的同学们写出了两个正确结论:①△APE为等腰直角三角形;②△APE的面积存在最小值.
学习任务:
①若BE=1,AB=$\sqrt{2}$,请你写出△APE面积的最小值为$\frac{3-2\sqrt{2}}{4}$(不要求进行说理);
②请你再写出一个有关△APE的正确结论:答案不唯一,如:在①的条件下,△APE的面积存在最大值,最大面积为$\frac{3+2\sqrt{2}}{4}$.
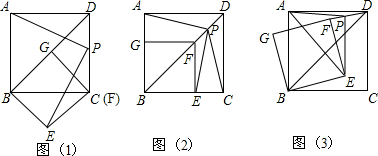
分析 独立思考:做出辅助线得到正方形,再判断出△ADP≌△PHE,即可;
合作交流:先判断出EH=HC,再判断出△ADP≌△CDP即可;
发现问题:①先判断出点E在边AB上时,AE最小,最后用等腰直角三角形的面积公式即可;
②先判断出AE越大,S△APE要越大,即点E在AB的延长线上时,AE最大,最后用等腰直角三角形的面积公式即可
解答 独立思考
证明:如图1,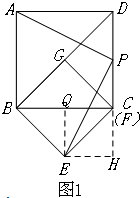
过点E作EH⊥DC,垂足为H,作EQ⊥BC,垂足为Q.
∵∠QEH=∠EHC=∠QCH=90°,
∴四边形QEHC为矩形.
又∵EQ=BQ=CQ
∴四边形QEHC为正方形,
∴EH=CQ=$\frac{1}{2}$BC.
又∵P为CD中点,DP=$\frac{1}{2}$DC;
∴DP=PC=CH=EH.
∴AD=PH.
又∵∠EHP=∠PDA=90°,
∴△ADP≌△PHE.
∴AP=PE,∠EPH=∠PAD.
∵∠PAD+∠APD=90°,
∴∠APD+EPH=90°.
∴AP⊥PE.
合作交流:“翱翔”小组的认识是正确的.
理由如下:如图2,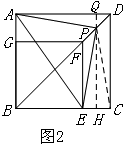
过点P作PH⊥BC于点H,并且交AD于点Q,则PQ⊥AD.
∴四边形QHCD是矩形,HQ∥CD.
连接PE,PC.
∵FE∥PH∥DC,
∴$\frac{FP}{PD}=\frac{EH}{CH}$.
∵FP=PD,
∴EH=HC.
∴PE=PC,∠EPH=∠HPC.
∵四边形ABCD为正方形,
∴∠ADP=∠CDP=45°.
又∵DP=DP,
∴△ADP≌△CDP.
∴AP=PC,∠PAQ=∠PCD.
∴AP=PE,
又∵∠HPC=∠PCD,
∴∠PAQ=∠EPH.
∵∠PAQ+∠APQ=90°,
∴∠EPH+∠APQ=90°.
∴AP⊥PE.
发现问题:如图3,
∵△APE为等腰直角三角形,且AP⊥DE,
∴斜边AE越小,S△APE要越小,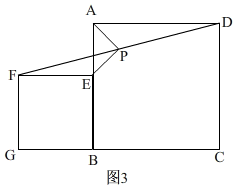
∴点E在边AB上时,AE最小,
∵AB=$\sqrt{2}$,BE=1,
∴AE=AB-BE=$\sqrt{2}$-1
∴S△APE最小值为$\frac{1}{2}$×$\frac{1}{2}$AE2=$\frac{1}{2}$×$\frac{1}{2}$×($\sqrt{2}$-1)2=$\frac{3-2\sqrt{2}}{4}$.
故答案为$\frac{3-2\sqrt{2}}{4}$.
②结论不唯一,如:在①的条件下,△APE的面积存在最大值,最大面积为$\frac{3+2\sqrt{2}}{4}$
理由:如图4,
∵△APE为等腰直角三角形,且AP⊥DE,
∴AE越大,S△APE要越大,
∴点E在AB的延长线上时,AE最大,
∵AB=$\sqrt{2}$,BE=1,
∴AE=AB+BE=$\sqrt{2}$+1
∴S△APE最小值为$\frac{1}{2}$×$\frac{1}{2}$AE2=$\frac{1}{2}$×$\frac{1}{2}$×($\sqrt{2}$+1)2=$\frac{3+2\sqrt{2}}{4}$.
故答案为:答案不唯一,如:在①的条件下,△APE的面积存在最大值,最大面积为$\frac{3+2\sqrt{2}}{4}$.
点评 此题是四边形综合题,主要考查了正方形的性质和判定,勾股定理,平行线分线段成比例定理,极值问题,解本题的关键是做出辅助线.

| A. | 2cm | B. | 4cm | C. | 2$\sqrt{2}$ cm | D. | $\sqrt{2}$ cm |
 一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:
一位农民带上若干千克自产的土豆进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题: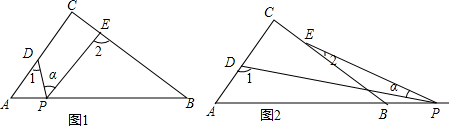
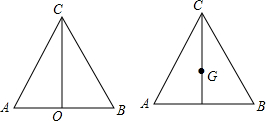
 如图,扇形OAB的圆心角∠AOB=120°,半径OA=6cm.
如图,扇形OAB的圆心角∠AOB=120°,半径OA=6cm.