题目内容
已知实数a满足
+
=a，求a-20132的值．（提示：a-2014≥0，即a≥2014）
| (2013-a)2 |
| a-2014 |
考点：二次根式的性质与化简,二次根式有意义的条件
专题：
分析：利用二次根式有意义的条件求出a的取值范围，利用二次根式的性质化简求出a的值，代入即可求出a-20132的值．
解答：解：根据二次根式有意义的条件可得a-2014≥0，解得a≥2014，
∵
+
=a，
∴a-2013+
=a，
∴
=2013，
∴a=20132+2014，
∴a-20132=2014．
∵
| (2013-a)2 |
| a-2014 |
∴a-2013+
| a-2014 |
∴
| a-2014 |
∴a=20132+2014，
∴a-20132=2014．
点评：本题主要考查了二次根式有意义的条件及二次根式的化简，解题的关键是利用二次根式有意义的条件求出a的取值范围．
练习册系列答案
相关题目
如图所示，点A是抛物线y=-x2上一点，AB⊥x轴于点B，若B点坐标为（-2，0），则A点坐标为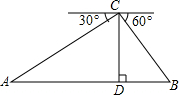
如图，四川汶川地区灾后修建铁路时，要建一条从A到B的隧道，测得山顶C到隧道的垂直高度CD为150m，从山顶C测得A点的俯角为30°，测得B点的俯角为60°，求隧道AB的长．