题目内容
12.已知f(x)=1+$\frac{1}{x}$,其中f(a)表示当x=a时代数式的值,如f(1)=1+$\frac{1}{1}$,f(2)=1+$\frac{1}{2}$,f(a)=1+$\frac{1}{a}$,则f(1)•f(2)•f(3)…•f(100)=101.分析 把数值代入,计算后交错约分得出答案即可.
解答 解:∵f(1)=1+$\frac{1}{1}$=2,f(2)=1+$\frac{1}{2}$=$\frac{3}{2}$,…f(a)=1+$\frac{1}{a}$=$\frac{a+1}{a}$,
∴f(1)•f(2)•f(3)…•f(100)
=2×$\frac{3}{2}$×$\frac{4}{3}$×…×$\frac{100}{99}$×$\frac{101}{100}$
=101.
故答案为:101.
点评 此题考查代数式求值,理解题意,计算出每一个式子的数值,代入求得答案即可.

练习册系列答案
相关题目
 如图,在△ABC中,PM、QN分别是AB、AC的垂直平分线,∠BAC=110°,BC=18,则∠PAQ=40°,则△APQ的周长为18.
如图,在△ABC中,PM、QN分别是AB、AC的垂直平分线,∠BAC=110°,BC=18,则∠PAQ=40°,则△APQ的周长为18.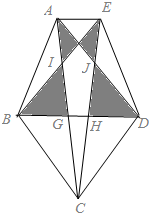 如图所示,三角形AEF,三角形BDF,三角形BCD都是正三角形,其中AE:BD=1:3,三角形AEF的面积是1,求阴影部分的面积.
如图所示,三角形AEF,三角形BDF,三角形BCD都是正三角形,其中AE:BD=1:3,三角形AEF的面积是1,求阴影部分的面积.