题目内容
19．
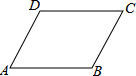如图，在平行四边形ABCD中，AB=8，BC=10cm，∠B=150°，则?ABCD的面积=40cm2．
分析 作平行四边形的高DE，由平行四边形的性质求出∠A=30°，由含30°角的直角三角形的性质求出DE，即可求出平行四边形的面积．
解答 解：作DE⊥AB于E，如图所示
∵四边形ABCD是平行四边形，
∴AD=BC=10cm，AD∥BC，
∴∠A+∠B=180°，
∴∠A=30°，
∴DE=$\frac{1}{2}$AD=5cm，
∴∠D=180-150=30°．
∴S?ABCD=AB•DE=8×5=40（cm2）．
故答案为：40cm2．
点评 本题考查了平行四边形的性质、含30°角的直角三角形的性质、平行四边形面积的计算；熟练掌握平行四边形的性质，求出AB边上的高DE是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
7．
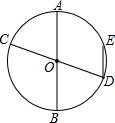如图，AB和CD是⊙O的两条直径，弦DE∥AB，若弧DE为40°的弧，则∠BOC=（ ）
如图，AB和CD是⊙O的两条直径，弦DE∥AB，若弧DE为40°的弧，则∠BOC=（ ）| A． | 110° | B． | 80° | C． | 40° | D． | 70° |
4．若（y+2）（y-5）=y2-my-10，则m的值为（ ）
| A． | 3 | B． | -3 | C． | 7 | D． | -7 |
11．下列运算正确的是（ ）
| A． | $\sqrt{4}=±2$ | B． | |-2|=-2 | C． | -22=4 | D． | $-\sqrt{4}=-2$ |
9．若点（-1，y1），（-2，y2），（2，y3）在反比例函数$y=-\frac{{{k^2}+1}}{x}$图象上，则下列结论正确的是（ ）
| A． | y1＞y2＞y3 | B． | y2＞y1＞y3 | C． | y3＞y1＞y2 | D． | y3＞y2＞y1 |