题目内容
7.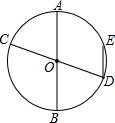 如图,AB和CD是⊙O的两条直径,弦DE∥AB,若弧DE为40°的弧,则∠BOC=( )
如图,AB和CD是⊙O的两条直径,弦DE∥AB,若弧DE为40°的弧,则∠BOC=( )| A. | 110° | B. | 80° | C. | 40° | D. | 70° |
分析 连接OE,根据弧、圆心角的关系求出∠DOE的度数,由等腰三角形的性质求出∠ODE的度数,根据平行线的性质得出∠AOC的度数,进而可得出∠BOC的度数.
解答  解:连接OE,
解:连接OE,
∵弧DE为40°的弧,
∴∠DOE=40°.
∵OD=OE,
∴∠ODE=$\frac{180°-40°}{2}$=70°.
∵弦DE∥AB,
∴∠AOC=∠ODE=70°,
∴∠BOC=180°-∠AOC=180°-70°=110°.
故选A.
点评 本题考查的是圆心角、弧、弦的关系,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
18.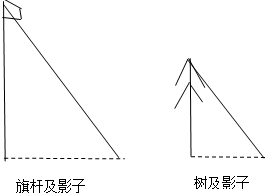 如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( )
如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( )
 如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( )
如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( )| A. | 4米 | B. | 2米 | C. | 1.8米 | D. | 3.6米 |
12.下列不等式是一元一次不等式的是( )
| A. | 5>-2 | B. | x<0 | C. | x+y>0 | D. | x2+x+9≥0 |
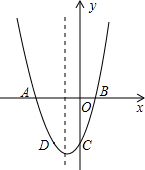 已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.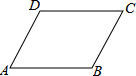 如图,在平行四边形ABCD中,AB=8,BC=10cm,∠B=150°,则?ABCD的面积=40cm2.
如图,在平行四边形ABCD中,AB=8,BC=10cm,∠B=150°,则?ABCD的面积=40cm2.