题目内容
若|a|=4，|b|=2，且a＜b，求a-b的值．
考点：有理数的减法,绝对值
专题：
分析：根据绝对值的性质求出a、b，再判断出a、b的对应情况，然后根据有理数的减法运算法则进行计算即可得解．
解答：解：∵|a|=4，|b|=2，
∴a=±4，b=±2，
∵a＜b，
∴a=-4，b=±2，
∴a-b=-4-2=-6，
或a-b=-4-（-2）=-4+2=-2，
所以，a-b的值为-2或-6．
∴a=±4，b=±2，
∵a＜b，
∴a=-4，b=±2，
∴a-b=-4-2=-6，
或a-b=-4-（-2）=-4+2=-2，
所以，a-b的值为-2或-6．
点评：本题考查了有理数的减法，绝对值的性质，熟记性质并求出a、b的值以及对应情况是解题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
函数y=-x2-1的开口方向和对称轴分别是（ ）
| A、向上，y轴 |
| B、向下，y轴 |
| C、向上，直线x=-1 |
| D、向下，直线x=-1 |
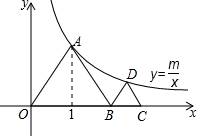如图，边长为2的等边三角形AOB的顶点在反比例函数y=| m |
| x |
A、
| ||||||
B、
| ||||||
C、2
| ||||||
D、2
|