题目内容
6.在平面直角坐标系xOy中,点M(m,$\frac{k}{m}$)(k>0的常数,且m>0).(1)若k=5,点M在直线y=x-4,求点M的坐标;
(2)若直线y=-x+b(b>0)与x轴、y轴分别交于点A和点B,点M在直线上有且只有一个位置,过点A与y轴平行的直线和过点B与x轴平行的直线交于点C,点M在直线AC上的点为点M1,点M在直线BC上的点为点M2,当S${\;}_{△O{M}_{1}{M}_{2}}$=k2+$\frac{5}{4}$k-$\frac{3}{8}$时,求线段M1M2的长.
分析 (1)根据k=5,点M在直线y=x-4,得到方程$\frac{5}{m}$=m-4,解方程求得m=5,可得点M的坐标为(5,1);
(2)点M与M1、M2的横坐标、纵坐标的关系的乘积:m×$\frac{k}{m}$=k,M1与A横坐标相同,所以M1(b,$\frac{k}{b}$),M2与B纵坐标相同,所以M2($\frac{k}{b}$,b),因为点M在直线y=-x+b(b>0)上有且只有一个位置,可得$\frac{k}{m}$=-m+b,可得b2=4k,再根据S${\;}_{△O{M}_{1}{M}_{2}}$=k2+$\frac{5}{4}$k-$\frac{3}{8}$可求线段M1M2的长.
解答 解:(1)∵k=5,点M在直线y=x-4,
∴$\frac{5}{m}$=m-4,
∴m=5,m=-1,
∵m>0,
∴m=5,
∴M(5,1);
(2)点M与M1、M2的横坐标、纵坐标的关系的乘积:m×$\frac{k}{m}$=k,
M1与A横坐标相同,所以M1(b,$\frac{k}{b}$),
M2与B纵坐标相同,所以M2($\frac{k}{b}$,b),
因为点M在直线y=-x+b(b>0)上有且只有一个位置,所以$\frac{k}{m}$=-m+b,
m2-bm+k=0,
△=b2-4k=0,b2=4k,
因为S${\;}_{△O{M}_{1}{M}_{2}}$=k2+$\frac{5}{4}$k-$\frac{3}{8}$,$\frac{1}{2}$($\frac{k}{b}$+b)($\frac{k}{b}$-b)=k2+$\frac{5}{4}$k-$\frac{3}{8}$,8k2+25k-3=0,
M1M2=2(b-$\frac{k}{b}$)2=2($\frac{{b}^{2}-k}{b}$)2=$\frac{9k}{2}$.
点评 考查了两条直线相交或平行问题,两条直线的平行问题,若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 5 | B. | -2 | C. | 5或-2 | D. | 以上都不对 |

| A. | 90 | B. | 91 | C. | 140 | D. | 141 |
 B.
B. 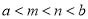
 D.
D. 
 如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.
如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.