题目内容
15.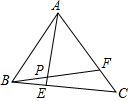 如图,△ABC中,E是BC上的一点,F是AC上一点,且3BE=BC,4CF=AF,AE、BF交于P点,如果△ABP的面积是30平方厘米,求△ABC的面积$\frac{120}{11}$.
如图,△ABC中,E是BC上的一点,F是AC上一点,且3BE=BC,4CF=AF,AE、BF交于P点,如果△ABP的面积是30平方厘米,求△ABC的面积$\frac{120}{11}$.
分析 过E作EG∥AC交BF于G,于是得到$\frac{GE}{CF}$=$\frac{BE}{BC}$,根据已知条件得到GE=$\frac{1}{12}$AF,根据相似三角形的性质得到$\frac{AP}{AE}$=$\frac{11}{12}$,于是得到结论.
解答  解:过E作EG∥AC交BF于G,
解:过E作EG∥AC交BF于G,
∴$\frac{GE}{CF}$=$\frac{BE}{BC}$,
∵3BE=BC,
∴GE=$\frac{1}{3}$CF,
∵4CF=AF,
∴GE=$\frac{1}{12}$AF,
∵GE∥AF,
∴△APF∽△GPE,
∴$\frac{AP}{PE}=\frac{GE}{AF}$=$\frac{1}{12}$,
∴$\frac{AP}{AE}$=$\frac{11}{12}$,
∵△ABP的面积是30平方厘米,
∴S△ABE=$\frac{360}{11}$,
∴S△ABC=3S△ABE=$\frac{120}{11}$.
故答案为:$\frac{120}{11}$.
点评 本题考查了三角形的面积的计算,相似三角形的判定和性质,掌握的作出辅助线是解题的关键.

练习册系列答案
相关题目
6.当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为( )
| A. | -$\frac{7}{4}$ | B. | $\sqrt{3}$或-$\sqrt{3}$ | C. | 2或-$\sqrt{3}$ | D. | 2或-$\sqrt{3}$或-$\frac{7}{4}$ |
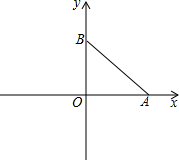 如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为
如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为
 如图,在平面直角坐标中,点O是坐标原点,一次函数y1=-x+4与反比例函数y2=$\frac{k}{x}$(x>0)的图象交于A(1,m)、B(n,1)两点.
如图,在平面直角坐标中,点O是坐标原点,一次函数y1=-x+4与反比例函数y2=$\frac{k}{x}$(x>0)的图象交于A(1,m)、B(n,1)两点.