题目内容
 如图,?ABCD中,四个内角的角平分线交于两点E,F,连接EF.
如图,?ABCD中,四个内角的角平分线交于两点E,F,连接EF.(1)求证:△ABE∽△CDF.
(2)若AD=8,AB=5,试求线段EF的长.
考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:(1)根据平行四边形的对角相等可得∠ABC=∠ADC,∠BAD=∠BCD,再根据角平分线的定义可得∠ABE=
∠ABC,∠CDF=
∠ADC,从而得到∠ABE=∠CDF,同理,∠BAE=∠DCF,然后根据两组角对应相等的两个三角形相似证明即可;
(2)延长AE交BC于G,根据平行四边形的邻角互补和角平分线的定义求出∠BAE+∠ABE=90°,再根据等腰三角形三线合一的性质可得AB=BG,根据等边对等角可得∠BAE=∠BGE,再求出∠BGE=∠BCF,然后求出四边形CFEG是平行四边形,根据平行四边形的对边相等可得EF=CG,然后求解即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)延长AE交BC于G,根据平行四边形的邻角互补和角平分线的定义求出∠BAE+∠ABE=90°,再根据等腰三角形三线合一的性质可得AB=BG,根据等边对等角可得∠BAE=∠BGE,再求出∠BGE=∠BCF,然后求出四边形CFEG是平行四边形,根据平行四边形的对边相等可得EF=CG,然后求解即可.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC,∠BAD=∠BCD,
∵点E、F是四个内角的平分线的交点,
∴∠ABE=
∠ABC,∠CDF=
∠ADC,
∴∠ABE=∠CDF,
同理,∠BAE=∠DCF,
∴△ABE∽△CDF;
(2)解:如图,延长AE交BC于G,
∵四边形ABCD是平行四边形,
∴∠ABC+∠BAD=180°,
∵点E、F是四个内角的平分线的交点,
∴∠BAE+∠ABE=
(∠BAD+∠ABC)=90°,
∴BE⊥AG,
又∵BE平分∠ABC,
∴AB=BG=5,AE=EG,
∴∠BAE=∠BGE,
∵CF平分∠BCD,
∴∠BCF=∠DCF,
∴∠BGE=∠BCF,
∴CF∥EG,
∵△ABE∽△CDF,AB=CD,
∴△ABE≌△CDF,
∴AE=CF,
∴EG=CF,
∴四边形CFEG是平行四边形,
∴EF=CG,
∵CG=BC-BG=8-5=3,
∴EF=3.
∴∠ABC=∠ADC,∠BAD=∠BCD,
∵点E、F是四个内角的平分线的交点,
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABE=∠CDF,
同理,∠BAE=∠DCF,
∴△ABE∽△CDF;
(2)解:如图,延长AE交BC于G,
∵四边形ABCD是平行四边形,
∴∠ABC+∠BAD=180°,
∵点E、F是四个内角的平分线的交点,
∴∠BAE+∠ABE=
| 1 |
| 2 |
∴BE⊥AG,
又∵BE平分∠ABC,
∴AB=BG=5,AE=EG,
∴∠BAE=∠BGE,

∵CF平分∠BCD,
∴∠BCF=∠DCF,
∴∠BGE=∠BCF,
∴CF∥EG,
∵△ABE∽△CDF,AB=CD,
∴△ABE≌△CDF,
∴AE=CF,
∴EG=CF,
∴四边形CFEG是平行四边形,
∴EF=CG,
∵CG=BC-BG=8-5=3,
∴EF=3.
点评:本题考查了平行四边形的性质,相似三角形的判定与性质,等腰三角形三线合一的性质,难在于(2)作辅助线构造出平行四边形.

练习册系列答案
相关题目
若一次函数y=(1-2k)x-k的图象经过第一、三、四象限,则k的取值范围是( )
A、k<
| ||
B、0<k<
| ||
C、0≤k<
| ||
D、k<0或k>
|
当实数x的取值使得
有意义时,函数y=-4x+1中y的取值范围是( )
| x-3 |
| A、y≥-11 |
| B、y≤-11 |
| C、y≥-13 |
| D、y≤-13 |
若代数式m2n3x-1与3nx+3m2是同类项,则x的值为( )
| A、-1 | B、1 | C、2 | D、3 |
 如图,直线l为一次函数y=kx+b的图象,则b=
如图,直线l为一次函数y=kx+b的图象,则b=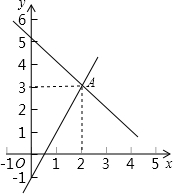 如图,点A的坐标可以看成是方程组
如图,点A的坐标可以看成是方程组