题目内容
已知m2=n+2,n2=m+2(m≠n),求m3-2mn+n3的值.
考点:因式分解的应用
专题:
分析:先由已知条件得出m+n的值,再把m2+2mn+n2化成完全平方的形式,再进行计算即可.
解答:解:由已知两式相减,得:m2-n2=n-m,
∴(m-n)(m+n+1)=0,
又∵m≠n,∴m+n=-1,
∴原式=m(n+2)-2mn+n(m+2)
=mn+2m-2mn+mn+2n
=2(m+n)
=-2.
∴(m-n)(m+n+1)=0,
又∵m≠n,∴m+n=-1,
∴原式=m(n+2)-2mn+n(m+2)
=mn+2m-2mn+mn+2n
=2(m+n)
=-2.
点评:本题考查了因式分解的应用,观察出已知条件得出m+n的值是解题的关键.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 如图,长方形内有两个四分之一圆.
如图,长方形内有两个四分之一圆.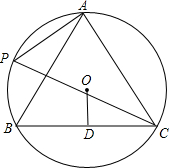 如图,A、P、B、C是半径为8的⊙O上的四点,且△ABC为等边三角形.
如图,A、P、B、C是半径为8的⊙O上的四点,且△ABC为等边三角形. 方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形,请你在图示的11×11的方格纸中,画出两个位似但不全等的格点三角形,并指出位似中心.(要求所画三角形是钝角三角形,并辨明相应字母)
方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形,请你在图示的11×11的方格纸中,画出两个位似但不全等的格点三角形,并指出位似中心.(要求所画三角形是钝角三角形,并辨明相应字母) 如图,圆柱的底面半径为2cm,点B距离底面8cm,从底面上的点绕曲面到达点B的最近距离
如图,圆柱的底面半径为2cm,点B距离底面8cm,从底面上的点绕曲面到达点B的最近距离