题目内容
1.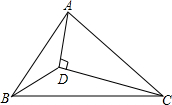 如图,在△ABC中,点D为△ABC内一点,连接AD,BD,CD,∠DBC=∠ACD=30°,∠ADC=90°,DB=3,BC=8,则AB的长为$\frac{10}{3}\sqrt{3}$.
如图,在△ABC中,点D为△ABC内一点,连接AD,BD,CD,∠DBC=∠ACD=30°,∠ADC=90°,DB=3,BC=8,则AB的长为$\frac{10}{3}\sqrt{3}$.
分析 过D作DP⊥BD,作∠BPD=30°,连接BP,CP,于是得到△DAC∽△DBP,根据相似三角形的性质得到$\frac{DB}{DP}=\frac{DA}{DC}$,由∠BDA=∠PDC,证得△BDA∽△PDC,在Rt△BDP中,确定BP=6,DP=3$\sqrt{3}$,CP=10,于是根据$\frac{AB}{CP}=\frac{DB}{DP}$,即可得到结论.
解答 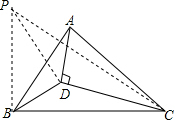 解:过D作DP⊥BD,作∠BPD=30°,连接BP,CP,
解:过D作DP⊥BD,作∠BPD=30°,连接BP,CP,
∴∠BDP=∠ADC=90°,∠BPD=∠ACD=30°,
∴△DAC∽△DBP,
∴$\frac{DB}{DP}=\frac{DA}{DC}$,
∵∠BDP+∠ADP=∠ADP+∠ADC,
∴∠BAD=∠PDC,
∴△BDA∽△PDC,
在Rt△BDP中,
∵∠BPD=30°,
∴BP=6,DP=3$\sqrt{3}$,∠PBD=60°,
∴∠PBC=60°+30°=90°,
∴CP=10,
∵$\frac{AB}{CP}=\frac{DB}{DP}$,
即AB=$\frac{3}{3\sqrt{3}}$×10=$\frac{10}{3}\sqrt{3}$.
故答案为:$\frac{10}{3}\sqrt{3}$.
点评 本题考查了相似三角形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.将抛物线y=3x2如何平移得到抛物线y=3(x-5)2+1( )
| A. | 向左平移5个单位,向下平移1个单位 | |
| B. | 向左平移5个单位,向上平移1个单位 | |
| C. | 向右平移5个单位,向下平移1个单位 | |
| D. | 向右平移5个单位,向上平移1个单位 |
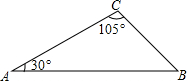 如图,已知AC=8,∠A=30°,∠C=105°,求AB和BC的长.
如图,已知AC=8,∠A=30°,∠C=105°,求AB和BC的长.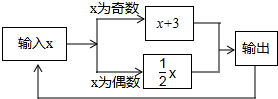 有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2015次输出的结果是4.
有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2015次输出的结果是4.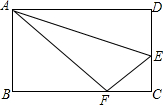 如图,把边长AD=10,AB=8的矩形沿AE对折,使点D落在BC上的点F处,求DE之长.
如图,把边长AD=10,AB=8的矩形沿AE对折,使点D落在BC上的点F处,求DE之长.