题目内容
3.已知(x3+mx+n)(x2-3x+1)展开后的结果中不含x3和x2项.(1)求m、n的值;
(2)求(m+n)(m2-mn+n2)的值.
分析 (1)原式利用多项式乘以多项式法则计算,根据结果中不含x3和x2项,求出m与n的值即可;
(2)原式利用多项式乘以多项式法则计算,将m与n的值代入计算即可求出值.
解答 解:(1)原式=x5-3x4+(m+1)x3+(n-3m)x2+(m-3n)x+n,
由展开式不含x3和x2项,得到m+1=0,n-3m=0,
解得:m=-1,n=-3;
(2)当m=-1,n=-3时,原式=m3-m2n+mn2+m2n-mn2+n3=m3+n3=-1-27=-28.
点评 此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
13.今年清明节期间,我市共接待游客48.6万人次,旅游收入218 000 000元.数据218 000 000用科学记数法表示为( )
| A. | 2.18×108 | B. | 0.218×109 | C. | 2.2×108 | D. | 2.2×109 |
14.已知某点向右平移3个单位长度,再向上平移3个单位长度得到坐标是(-1,4),则该点平移前坐标是( )
| A. | (-4,1) | B. | (-4,7) | C. | (2,2) | D. | (2,7) |
12.在实数O、n、$\frac{22}{7}$、$\sqrt{2}$、-$\sqrt{4}$中,无理数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
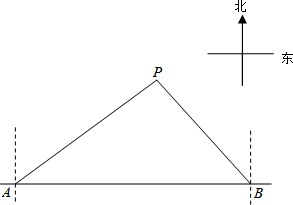 马航MH370失联后,我国政府积极参与搜救,某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东60°方向上,在救助船B的西北方向上,船B在船A正东方向81海里处.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
马航MH370失联后,我国政府积极参与搜救,某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东60°方向上,在救助船B的西北方向上,船B在船A正东方向81海里处.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)