题目内容
15.已知不等式$\frac{1}{3}$(x-m)>2-m.(1)若上面不等式的解集为x>3,求m的值.
(2)若满足x>3的每一个数都能使上面的不等式成立,求m的取值范围.
分析 (1)先把m当作已知条件表示出x的取值范围,再与不等式的解集为x>3相比较即可得出m的值;
(2)根据满足x>3的每一个数不等式成立可得出关于m的不等式,求出m的取值范围即可.
解答 解:(1)解不等式可得x>6-2m,
∵不等式的解集为x>3,
∴6-2m=3,解得m=$\frac{3}{2}$;
(2)∵原不等式可化为x>6-2m,满足x>3的每一个数都能使不等式成立,
∴6-2m≤3,解得m≥$\frac{3}{2}$.
点评 本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20.2015年央视春晚微信摇一摇互动总量达110亿次,将110亿用科学记数法表示为( )
| A. | 110×108 | B. | 11×109 | C. | 1.1×1010 | D. | 1.1×1011 |
7. 如图,实数-3,x,3,y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最大的数对应的点是( )
如图,实数-3,x,3,y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最大的数对应的点是( )
 如图,实数-3,x,3,y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最大的数对应的点是( )
如图,实数-3,x,3,y在数轴上的对应点分别为M、N、P、Q,这四个数中绝对值最大的数对应的点是( )| A. | 点M | B. | 点N | C. | 点P | D. | 点Q |
5. 如图是一几何体的三视图,这个几何体可能是( )
如图是一几何体的三视图,这个几何体可能是( )
 如图是一几何体的三视图,这个几何体可能是( )
如图是一几何体的三视图,这个几何体可能是( )| A. | 三棱柱 | B. | 三棱锥 | C. | 圆柱 | D. | 圆锥 |
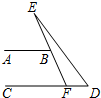 如图,AB∥CD,∠ABE=60°,则∠EFD的度数为120°.
如图,AB∥CD,∠ABE=60°,则∠EFD的度数为120°.