题目内容
6.如图,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线l(1)作BD⊥l于点D,CE⊥l于E点,若B点和C点在直线l的同侧,求证:DE=BD+CE;
(2)若直线l绕点A旋转到B点和C点在其西侧,其余条件不变,问:BD、DE、CE的关系如何?请予以证明.
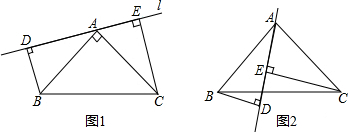
分析 (1)由AAS证明△ABD≌△CAE,得到BD=AE,AD=CE,即可解决问题.
(2)由AAS证明证明△ABD≌△CAE,得出BD=AE,AD=CE,即可得出结论.
解答 (1)证明:∵∠BAC=90°,BD⊥DE,CE⊥DE,
∴∠DAB+∠DBA=∠DAB+∠EAC,
∴∠DBA=∠EAC;
在△ABD与△CAE中,$\left\{\begin{array}{l}{∠DBA=∠EAC}&{\;}\\{∠BDA=∠AEC}&{\;}\\{AB=AC}&{\;}\end{array}\right.$,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴DE=BD+CE.
(2)解:CE=BD+DE;理由如下:
同(1)得:∠ABD=∠CAE,
在△ABD和△CAE中,$\left\{\begin{array}{l}{∠ABD=∠CAE}&{\;}\\{∠ADB=∠CEA}&{\;}\\{AB=AC}&{\;}\end{array}\right.$,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD=AE+DE,
∴CE=BD+DE.
点评 该题主要考查了全等三角形的判定及其性质、等腰直角三角形的性质;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
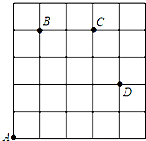 如图,蚂蚁在5×5的方格(每小方格边长为1cm)上沿着网格线运动.它从A处出发去寻找B、C、D处的其他伙伴,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
如图,蚂蚁在5×5的方格(每小方格边长为1cm)上沿着网格线运动.它从A处出发去寻找B、C、D处的其他伙伴,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中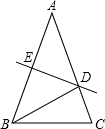 如图,△ABC中,AB=AC=5.AB的垂直平分线DE交AB、AC于E、D,△BCD的周长为8,则△ABC的周长是13.
如图,△ABC中,AB=AC=5.AB的垂直平分线DE交AB、AC于E、D,△BCD的周长为8,则△ABC的周长是13.