题目内容
 如图所示,已知EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线,
如图所示,已知EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线,(1)若∠AOC:∠COF=4:7,求∠DOF的大小
(2)若∠AOC:∠DOH=8:29,求∠COH.
考点:垂线,角平分线的定义
专题:
分析:(1)由EF⊥AB,可得出∠AOF=90°,结合∠AOC:∠COF=4:7,可得出∠AOC,由对顶角相等即可得出∠DOF的度数.
(2)由∠DOB═90°-2∠COG,∠DOB:[
(180°-∠COG]=8:29组成方程即可得出,∠COG的度数,代入求出∠DOH,即可求出∠COH.
(2)由∠DOB═90°-2∠COG,∠DOB:[
| 1 |
| 2 |
解答:解:(1)∵EF⊥AB,
∴∠AOF=90°,
∵∠AOC:∠COF=4:7,
∴∠AOC=
∠AOF=
×90°=(
)°,
∵∠BOD=∠AOC
∴∠DOF=∠FOB+∠BOD=90°+(
)°=(
)°,
(2)∵∠AOC=∠DOB,
∴∠DOB=90°-2COF=90°-2∠COG,
∵OH为∠DOG的平分线,
∴
(180°-∠COG)=∠DOH,
∵∠AOC:∠DOH=8:29,
∴∠DOB:[
(180°-∠COG]=8:29,
解得∠DOB=20°,∠COG=35°,
∴
(180°-∠COG)=∠DOH=72.5°,
∴∠COH=180°-72.5°=107.5°.
∴∠AOF=90°,
∵∠AOC:∠COF=4:7,
∴∠AOC=
| 4 |
| 11 |
| 4 |
| 11 |
| 360 |
| 11 |
∵∠BOD=∠AOC
∴∠DOF=∠FOB+∠BOD=90°+(
| 360 |
| 11 |
| 1350 |
| 11 |
(2)∵∠AOC=∠DOB,
∴∠DOB=90°-2COF=90°-2∠COG,
∵OH为∠DOG的平分线,
∴
| 1 |
| 2 |
∵∠AOC:∠DOH=8:29,
∴∠DOB:[
| 1 |
| 2 |
解得∠DOB=20°,∠COG=35°,
∴
| 1 |
| 2 |
∴∠COH=180°-72.5°=107.5°.
点评:本题主要考查了垂线及角平分线的定义,解题的关键是根据垂线及角平分线的定义列出式子求解.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
在下列实数
,0.101001,
,
-1,
,
中无理数有( )
| 22 |
| 7 |
| 8 |
| 2 |
| 36 |
| π |
| 3 |
| A、3个 | B、4个 | C、5个 | D、6个 |
在平面直角坐标系中,以点(2,3)为圆心、3为半径的圆,一定( )
| A、与x轴相切,与y轴相切 |
| B、与x轴相切,与y轴相交 |
| C、与x轴相交,与y轴相切 |
| D、与x轴相交,与y轴相交 |

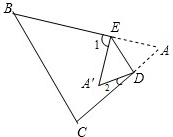 如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部.
如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部. 如图所示,已知四边形ABCD内接于⊙O,A是弧BAC的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且BF=AD,EM切⊙O于M.
如图所示,已知四边形ABCD内接于⊙O,A是弧BAC的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且BF=AD,EM切⊙O于M.