题目内容
4.证明:从圆外一点可以引两条切线,它们的切线长相等,这一点和圆心的连线,平分两条切线的夹角,平分两条切线的夹角.(画出图形,写出已知,求证并证明.)分析 利用切线的性质结合全等三角形的判定方法得出Rt△OPA≌Rt△OPB即可得出答案.
解答 已知:PA,PB是⊙O的切线,
求证:PA=PB,∠APO=∠BPO.
证明:连接OA,OB,
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
在Rt△OPA和Rt△OPB中
$\left\{\begin{array}{l}{OP=OP}\\{OA=OB}\end{array}\right.$,
∴Rt△OPA≌Rt△OPB(HL),
∴PA=PB,∠APO=∠BPO.
点评 此题主要考查了切线的性质以及切线长定理的证明,得出Rt△OPA≌Rt△OPB是解题关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
16.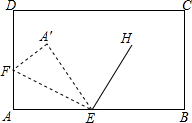 如图,将一长方形纸片一角斜折,使点A落在A′处,折痕为EF,EH平分∠A′EB,则∠FEH的度数为( )
如图,将一长方形纸片一角斜折,使点A落在A′处,折痕为EF,EH平分∠A′EB,则∠FEH的度数为( )
 如图,将一长方形纸片一角斜折,使点A落在A′处,折痕为EF,EH平分∠A′EB,则∠FEH的度数为( )
如图,将一长方形纸片一角斜折,使点A落在A′处,折痕为EF,EH平分∠A′EB,则∠FEH的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 95° |
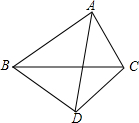 已知:如图,△ABC,BD=CD,AD平分∠BAC,求证:∠BAC+∠BDC=180°.
已知:如图,△ABC,BD=CD,AD平分∠BAC,求证:∠BAC+∠BDC=180°.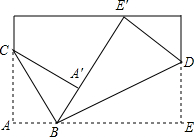 同学们,你玩过折纸游戏吗?折纸游戏里还蕴藏着不少数学知识呢!请准备一张长方形纸片,按照小亮的方法折纸,折叠后A′B与E′B在同一直线上,如图所示,则两折痕BC与BD的夹角∠CBD的度数为90°.
同学们,你玩过折纸游戏吗?折纸游戏里还蕴藏着不少数学知识呢!请准备一张长方形纸片,按照小亮的方法折纸,折叠后A′B与E′B在同一直线上,如图所示,则两折痕BC与BD的夹角∠CBD的度数为90°.