��Ŀ����
��m2+2mn+2n2-6n+9=0����
��ֵ
�⣺��m2+2mn+2n2-6n+9=0�ࣨm+n��2+��n-3��2=0
�ࣨm+n��2=0 ��n-3��2=0
��n=3 m=-3
��
=
=-
������Ĺ۲죬̽���������⣺
��1����֪x2+2y2-2xy+2y+1=0����x+2y��ֵ��
��2����֪a��b��c�ǡ�ABC�����ߣ�������a2+b2-8b-10a+41=0�����ABC�����c��ȡֵ��Χ��
| m |
| n2 |
�⣺��m2+2mn+2n2-6n+9=0�ࣨm+n��2+��n-3��2=0
�ࣨm+n��2=0 ��n-3��2=0
��n=3 m=-3
��
| m |
| n2 |
| -3 |
| 32 |
| 1 |
| 3 |
������Ĺ۲죬̽���������⣺
��1����֪x2+2y2-2xy+2y+1=0����x+2y��ֵ��
��2����֪a��b��c�ǡ�ABC�����ߣ�������a2+b2-8b-10a+41=0�����ABC�����c��ȡֵ��Χ��
���㣺��ʽ�ֽ��Ӧ��
ר�⣺
��������1�����Ȱ�x2+2y2-2xy+2y+1=0������ȫƽ����ʽ��ʽ�ֽ⣬���÷Ǹ������������x��y���������ֵ��
��2��������ȫƽ����ʽ��a2+b2-8b-10a+41=0��ʽ�ֽ⣬��һ�����÷Ǹ������������a��b����һ�����������ε����߹�ϵ��ô𰸼��ɣ�
��2��������ȫƽ����ʽ��a2+b2-8b-10a+41=0��ʽ�ֽ⣬��һ�����÷Ǹ������������a��b����һ�����������ε����߹�ϵ��ô𰸼��ɣ�
����⣺��1����x2+2y2-2xy+2y+1=0
��x2-2xy+y2+y2+2y+1=0
�ࣨx-y��2+��y+1��2=0
�ࣨx-y��2=0����y+1��2=0
��x=-1��y=-1
��x+2y=-3
��2����a2+b2-8b-10a+41=0
��a2-10a+25+b2-8b+16=0
�ࣨa-5��2+��b-4��2=0
�ࣨa-5��2=0����b-4��2=0
��a=5��b=4
��a��b��c�ǡ�ABC������
��1��c��9
��c������
��5��c��9��
��x2-2xy+y2+y2+2y+1=0
�ࣨx-y��2+��y+1��2=0
�ࣨx-y��2=0����y+1��2=0
��x=-1��y=-1
��x+2y=-3
��2����a2+b2-8b-10a+41=0
��a2-10a+25+b2-8b+16=0
�ࣨa-5��2+��b-4��2=0
�ࣨa-5��2=0����b-4��2=0
��a=5��b=4
��a��b��c�ǡ�ABC������
��1��c��9
��c������
��5��c��9��
���������⿼��������ȫƽ����ʽ��ʽ�ֽ⣬�Լ��Ǹ��������ʵ����ã�

��ϰ��ϵ�д�
 ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
�����Ŀ
�����ʽ����
-
=
������������m��ֵ�ǣ�������
| 2x |
| x+1 |
| m+1 |
| x2+x |
| x+1 |
| x |
| A��-1��-2 | B��-1��2 |
| C��1��2 | D��1��-2 |
 ��ͼ���ڡ�ABC�У���C=90�㣬��A=25�㣬�Ե�CΪԲ�ģ�BCΪ�뾶��Բ��AB�ڵ�D����AC�ڵ�E����
��ͼ���ڡ�ABC�У���C=90�㣬��A=25�㣬�Ե�CΪԲ�ģ�BCΪ�뾶��Բ��AB�ڵ�D����AC�ڵ�E����
 ��ͼ��������AEFG�Ķ���E��G��������ABCD�ı�AB��AD�ϣ�����BF��DF��
��ͼ��������AEFG�Ķ���E��G��������ABCD�ı�AB��AD�ϣ�����BF��DF��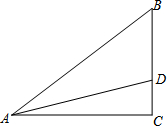 ��ͼ����Rt��ABC�У���֪��C=90�㣬
��ͼ����Rt��ABC�У���֪��C=90�㣬