题目内容
5.阅读下面材料:学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪想:要想解决问题,应该对∠B进行分类研究.
∠B可分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当∠B是直角时,如图1,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是C;
A.全等 B.不全等 C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°,求证:△ABC≌△DEF.

分析 第二种情况:以F为圆心,AC长为半径画弧,交射线EM于D、D′;则DF=D′F=AC,△DEF≌△ABC,△D′EF和△ABC不全等;
第三种情况:过点C作CG⊥AB交AB的延长线于点G,过点F作DH⊥DE交DE的延长线于点H,先证明△CBG≌△FEH,得出CG=FH,再证明Rt△ACG≌Rt△DFH,得出∠A=∠D,再由AAS即可证出△ABC≌△DEF.
解答 解:第二种情况:如图1所示: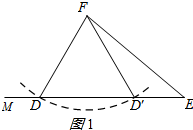
以F为圆心,AC长为半径画弧,交射线EM于D、D′;
则DF=D′F=AC,△DEF≌△ABC,△D′EF和△ABC不全等;
故选:C;
第三种情况:
证明:如图2所示:
过点C作CG⊥AB交AB的延长线于点G,
过点F作DH⊥DE交DE的延长线于点H,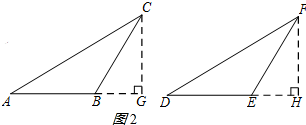
∵∠B=∠E,
∴180°-∠B=180°-∠E,
即∠CBG=∠FEH,
在△CBG和△FEH中,
$\left\{{\begin{array}{l}{∠CBG=∠FEH}\\{∠G=∠H=90°}\\{BC=EF}\end{array}}\right.$,
∴△CBG≌△FEH(AAS),
∴CG=FH,
在Rt△ACG和Rt△DFH中,$\left\{{\begin{array}{l}{AC=DF}\\{CG=FH}\end{array}}\right.$,
∴Rt△ACG≌Rt△DFH(HL),
∴∠A=∠D,
在△ABC和△DEF中,$\left\{{\begin{array}{l}{∠A=∠D}\\{∠B=∠E}\\{AC=DF}\end{array}}\right.$,
∴△ABC≌△DEF(AAS).
点评 本题考查了全等三角形的判定与性质;熟练掌握三角形全等的判定方法,证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.能判定四边形ABCD为平行四边形的条件是( )
| A. | AB=AD,CB=CD | B. | ∠A=∠B,∠C=∠D | C. | AB=CD,AD=BC | D. | AB∥CD,AD=BC |
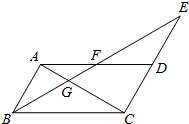 如图,在?ABCD中,延长CD到E,使DE=CD,连接BE,交AD于点F,交AC于点G.
如图,在?ABCD中,延长CD到E,使DE=CD,连接BE,交AD于点F,交AC于点G.
 在平面直角坐标系xOy中,抛物线y=ax2+bx+1(a≠0)过点A(-1,0),B(1,1),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=ax2+bx+1(a≠0)过点A(-1,0),B(1,1),与y轴交于点C.