题目内容
14.化简:$(\frac{x+2}{{{x^2}-2x}}-\frac{x-1}{{{x^2}-4x+4}})÷\frac{x-4}{x}$,然后请自选一个你喜欢的x值,再求原式的值.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x=1代入计算即可求出值.
解答 解:原式=[$\frac{(x+2)(x-2)}{x(x-2)^{2}}$-$\frac{x(x-1)}{x(x-2)^{2}}$]•$\frac{x}{x-4}$
=$\frac{{x}^{2}-4-{x}^{2}+x}{x(x-2)^{2}}$•$\frac{x}{x-4}$
=$\frac{x-4}{x(x-2)^{2}}$•$\frac{x}{x-4}$
=$\frac{1}{(x-2)^{2}}$,
当x=1时,原式=1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.-3的倒数是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
2.如图是用火柴棒摆出的一系列三角形图案,按这种方式摆下去,则所用的火车棒的根数y(根)与所摆图案的层数x(层)之间的关系可通过下表来探究.
每当所摆图案的层数x取一个定值时,所用火柴棒的根数y就随之确定,y与x的函数关系式是y=$\frac{3}{2}$x(x+1).
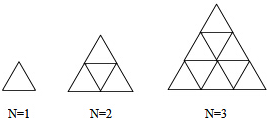
| x/层 | 1 | 2 | 3 | 4 | 5 | … |
| y/根 | 3 | 9 | 18 | 30 | 45 | … |
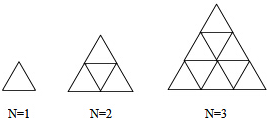
6.下列手机软件图标中,属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
