题目内容
分解因式．
①x2-4y2+x-2y
②1-x2+2xy-y2．
①x2-4y2+x-2y
②1-x2+2xy-y2．
考点：因式分解-分组分解法
专题：
分析：①将前两项利用平方差公式分解因式，进而利用提取公因式法分解因式；
②将后三项利用完全平方公式分解因式，进而利用平方差公式分解因式即可．
②将后三项利用完全平方公式分解因式，进而利用平方差公式分解因式即可．
解答：解：①x2-4y2+x-2y
=（x+2y）（x-2y）+x-2y
=（x-2y）（x+2y+1）；
②1-x2+2xy-y2
=1-（x-y）2
=（1-x+y）（1+x-y）．
=（x+2y）（x-2y）+x-2y
=（x-2y）（x+2y+1）；
②1-x2+2xy-y2
=1-（x-y）2
=（1-x+y）（1+x-y）．
点评：此题主要考查了分组分解法以及公式法分解因式，正确应用乘法公式是解题关键．
练习册系列答案
相关题目
一件工作，甲单独完成需要m小时，甲、乙合作需要n小时，则乙单独完成需要的时间为（ ）
| A、m-n | ||
B、
| ||
C、
| ||
D、
|
方程x2+2ax+a-1=0的根的情况是（ ）
| A、有两个相等的实数 |
| B、没有实数根 |
| C、有两个不相等的实数根 |
| D、不能确定 |
如图所示，它是小孔成像的原理，根据图中尺寸（AB∥CD），如果已知物体AB=30，则CD的长应是（ ）| A、15 | B、30 | C、20 | D、10 |
如图，A，B两点的坐标分别是A（1，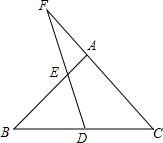
如图，已知在△ABC中，AB=AC=10，BC=16，D是BC中点，E是射线BA上一动点，直线DE交射线CA于F，当DF=DC时，求AF的值．