题目内容
已知 A(x1,y1),B(x2,y2)是反比例函数y=-
图象上的两点,且x2-x1=-2,x1•x2=3.
(1)在图中用“描点”的方法作出此反比例函数的图象;
(2)求y1-y2的值及点A的坐标;
(3)若-4<y≤-1,依据图象写出x的取值范围.
| 2 |
| x |
(1)在图中用“描点”的方法作出此反比例函数的图象;
(2)求y1-y2的值及点A的坐标;
(3)若-4<y≤-1,依据图象写出x的取值范围.
考点:反比例函数图象上点的坐标特征,反比例函数的图象,反比例函数的性质
专题:计算题
分析:(1)利用描点法画函数图象;
(2)利用反比例函数图象上点的坐标特征得到y1-y2=-
-(-
),再通分后把x2-x1=-2,x1•x2=3代入计算即可得到y1-y2的值;然后消去x2得到关于x1的方程x12+2x1-3=0,解方程得到x1的值,再计算对应的函数值即可得到A点坐标;
(3)观察函数图象得到当
<x≤2时,对应的函数值为-4<y≤-1.
(2)利用反比例函数图象上点的坐标特征得到y1-y2=-
| 2 |
| x1 |
| 2 |
| x2 |
(3)观察函数图象得到当
| 1 |
| 2 |
解答:解(1)反比例函数的图象如图,

(2)∵x1-x2=-2,x1•x2=3,
∴y1-y2=-
-(-
)=
=
=-
;
由x1-x2=-2得x1=x2-2,代入x1•x2=3得:x12+2x1-3=0,解得x1=1或x1=-3,
当x1=1时,y1=-
=-2;
当x1=-3时,y1=-
=
,
∴点A的坐标(1,-2)或(-3,
);
(3)如图,当-4<y≤-1时,x的取值范围为
<x≤2.

(2)∵x1-x2=-2,x1•x2=3,
∴y1-y2=-
| 2 |
| x1 |
| 2 |
| x2 |
| 2(x1-x2) |
| x1x2 |
| 2×(-2) |
| 3 |
| 4 |
| 3 |
由x1-x2=-2得x1=x2-2,代入x1•x2=3得:x12+2x1-3=0,解得x1=1或x1=-3,
当x1=1时,y1=-
| 2 |
| 1 |
当x1=-3时,y1=-
| 2 |
| -3 |
| 2 |
| 3 |
∴点A的坐标(1,-2)或(-3,
| 2 |
| 3 |
(3)如图,当-4<y≤-1时,x的取值范围为
| 1 |
| 2 |
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了反比例函数的性质.
| k |
| x |

练习册系列答案
相关题目
下列说法错误的是( )
| A、单项式与多项式统称为整式 |
| B、相等的角是对顶角 |
| C、两个负数比较大小绝对值大的反而小 |
| D、同角的补角相等 |
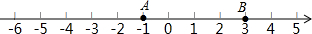 已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.
已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.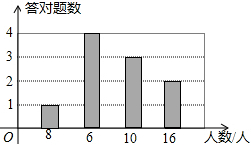 电视台在某次青年歌手大奖赛中,设置了基本知识问答题,答对一题得5分,答错或不答得0分,统计结果如图所示.
电视台在某次青年歌手大奖赛中,设置了基本知识问答题,答对一题得5分,答错或不答得0分,统计结果如图所示. 如图,在△ABC中,D,E分别是AB,AC上的点,AF平分∠BAC,交DE于点G,交BC于点F.若∠AED=∠B,且AG:GF=2:1,则DE:BC=
如图,在△ABC中,D,E分别是AB,AC上的点,AF平分∠BAC,交DE于点G,交BC于点F.若∠AED=∠B,且AG:GF=2:1,则DE:BC=