题目内容
5.阅读下列材料:一般地,n个相同的因数a相乘:a×a×a×a×…×a记作an,如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).此时,3叫做以2为底8的对数,记为log28(log28=3).一般地,若an=b,则n叫做以a为底的b的对数,记为logab=n,如34=81,则4叫做以3为底的81的对数,记为log381=4.
(1)下列各对数的值:log24=2;log216=4;log264=6;
(2)观察(1)中三数4,16,64之间满足怎样的关系式,写出log24,log216,log264满足的关系式log24+log216=log264;
(3)由(2)的结果,你能归纳出一个一般性的结果吗?logaM+logaN=logaMN;(a>0且a≠1,M>0,N>0)
(4)根据上述结论解决下列问题:
已知,loga2=0.3,求loga4和loga8的值.(a>0且a≠1)
分析 根据题目给出的定义即可求出答案.
解答 解:(1)∵22=4,24=16,26=64
∴log24=2;log216=4,log264=6
(2)log24+log216=log2(4×16)=log264
(3)logaM+logaN=logaMN
(4)loga2+loga2=loga4=0.3+0.3=0.6,
loga2+loga4=loga8=0.6+0.3=0.9
故答案为:(1)2;4;6
(2)log24+log216=log264
(3)logaMN
点评 本题考查学生的阅读理解能力,涉及同底数幂的乘法,解决本题的关键是利用同底数幂的乘法,属于中等题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.化简(1+$\frac{1}{x-2}$)÷$\frac{x-1}{{x}^{2}-4x+4}$的结果是( )
| A. | x+2 | B. | x-1 | C. | $\frac{1}{x+2}$ | D. | x-2 |
18.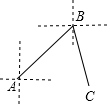 如图所示,一艘船在海上从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东20°方向行至点C,则∠ABC的度数是( )
如图所示,一艘船在海上从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东20°方向行至点C,则∠ABC的度数是( )
 如图所示,一艘船在海上从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东20°方向行至点C,则∠ABC的度数是( )
如图所示,一艘船在海上从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东20°方向行至点C,则∠ABC的度数是( )| A. | 45° | B. | 65° | C. | 75° | D. | 90° |
 如图,锐角三角形ABC中,∠A,∠B,∠C的对边分别是a,b,c,已知二次函数y═x2cosA-x+$\frac{1}{cosA}$的图象顶点与点(-2cosA,3cosA)关于y轴对称.延长AB到P,使AP=2AC,若以C为圆心,AC为半径的圆与以B为圆心、BP为半径的圆相外切.
如图,锐角三角形ABC中,∠A,∠B,∠C的对边分别是a,b,c,已知二次函数y═x2cosA-x+$\frac{1}{cosA}$的图象顶点与点(-2cosA,3cosA)关于y轴对称.延长AB到P,使AP=2AC,若以C为圆心,AC为半径的圆与以B为圆心、BP为半径的圆相外切. 如图,已知四边形ABCD中∠1=∠2,AB=CD=3,BC=5,求四边形ABCD的周长.
如图,已知四边形ABCD中∠1=∠2,AB=CD=3,BC=5,求四边形ABCD的周长.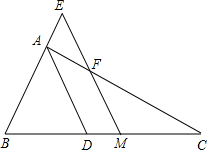 如图,△ABC中∠A的平分线为AD,M为BC的中点,过点M作ME∥AD交BA的延长线于E,交AC于F.
如图,△ABC中∠A的平分线为AD,M为BC的中点,过点M作ME∥AD交BA的延长线于E,交AC于F. 如图,△ABC中,AB=AC=10,∠BAC=30°,现将△ABC绕点A逆时针旋转30°得到△ACD,延长AD,BC相交于点E,则DE的长是5$\sqrt{3}$-5.
如图,△ABC中,AB=AC=10,∠BAC=30°,现将△ABC绕点A逆时针旋转30°得到△ACD,延长AD,BC相交于点E,则DE的长是5$\sqrt{3}$-5.