题目内容
18.数轴上A点读数为-1,B点读为3,点C在数轴上,且AC+BC=6,则C点的读数为( )| A. | -2 | B. | 4 | C. | -2或4 | D. | -3或5 |
分析 根据题意,可以分三种情况对点C进行讨论,然后根据AC+BC=6,求出相应的带你C的读数,从而可以解答本题.
解答 解:当点C在点A的左侧时,设点C的读数为c1,
∵AC+BC=6,
∴(-1-c1)+(3-c1)=6,
解得,c1=-2;
当点C在点A和B中间时,设点C的读数为c2,
∵∵AC+BC=6,
∴[c2-(-1)]+(3-c2)=6,
化简,得4=6
∵4=4不成立,
∴点C在点A和B中间时不成立;
当点C在点B的右侧时,设点C的读数为c3,
∵AC+BC=6,
∴[c3-(-1)]+(c3-3)=6,
解得,c3=4;
由上可得,点C的读数是-2或4,
故选C.
点评 本题考查数轴,解答此类问题的关键是明确数轴的特点,利用分类讨论的数学思想解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )
如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )
 如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )
如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
13.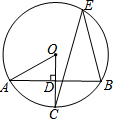 如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
 如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
3.已知正方体的体积为2$\sqrt{2}$,则这个正方体的棱长为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 3 |
10.面积为2的正方形的边长在( )
| A. | 1.5和2之间 | B. | 1和1.5之间 | C. | 0.5和1之间 | D. | 0和0.5之间 |
7.估计$\sqrt{48}$-$\frac{\sqrt{27}}{3}$的运算结果在( )
| A. | 3和4之间 | B. | 4和5之间 | C. | 5和6之间 | D. | 6和7之间 |
8.下列计算正确的是( )
| A. | $\sqrt{(-4)^{2}}$=-4 | B. | (a2)3=a5 | C. | a•a3=a4 | D. | 2a-a=2 |
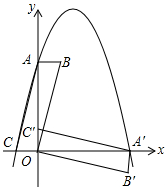 在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.