题目内容
 如图,菱形ABCD和菱形ECGF的边BC、CG在同一直线上,∠A=120°,AB=4,EF=6,则阴影部分的面积是________.
如图,菱形ABCD和菱形ECGF的边BC、CG在同一直线上,∠A=120°,AB=4,EF=6,则阴影部分的面积是________.
4
分析:设BF交CE于点H,根据菱形的对边平行,利用相似三角形对应边成比例列式求出CH,然后求出DH,根据菱形邻角互补求出∠ABC=60°,再求出点B到CD的距离以及点G到CE的距离;然后根据阴影部分的面积=S△BDH+S△FDH,根据三角形的面积公式列式进行计算即可得解.
解答: 解:如图,设BF交CE于点H,
解:如图,设BF交CE于点H,
∵菱形ECGF的边CE∥GF,
∴△BCH∽△BGF,
∴ =
= ,
,
即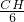 =
=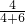 ,
,
解得CH= ,
,
所以,DH=CD-CH=4- =
= ,
,
∵∠A=120°,
∴∠ECG=∠ABC=180°-120°=60°,
∴点B到CD的距离为4× =2
=2 ,
,
点G到CE的距离为6× =3
=3 ,
,
∴阴影部分的面积=S△BDH+S△FDH,
= ×
× ×2
×2 +
+ ×
× ×3
×3 ,
,
=4 .
.
故答案为:4 .
.
点评:本题考查了菱形的对边平行,邻角互补的性质,相似三角形对应边成比例的性质,求出DH的长度,把阴影部分的面积分成两个三角形的面积进行求解是解题的关键.

分析:设BF交CE于点H,根据菱形的对边平行,利用相似三角形对应边成比例列式求出CH,然后求出DH,根据菱形邻角互补求出∠ABC=60°,再求出点B到CD的距离以及点G到CE的距离;然后根据阴影部分的面积=S△BDH+S△FDH,根据三角形的面积公式列式进行计算即可得解.
解答:
 解:如图,设BF交CE于点H,
解:如图,设BF交CE于点H,∵菱形ECGF的边CE∥GF,
∴△BCH∽△BGF,
∴
 =
= ,
,即
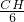 =
=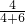 ,
,解得CH=
 ,
,所以,DH=CD-CH=4-
 =
= ,
,∵∠A=120°,
∴∠ECG=∠ABC=180°-120°=60°,
∴点B到CD的距离为4×
 =2
=2 ,
,点G到CE的距离为6×
 =3
=3 ,
,∴阴影部分的面积=S△BDH+S△FDH,
=
 ×
× ×2
×2 +
+ ×
× ×3
×3 ,
,=4
 .
.故答案为:4
 .
.点评:本题考查了菱形的对边平行,邻角互补的性质,相似三角形对应边成比例的性质,求出DH的长度,把阴影部分的面积分成两个三角形的面积进行求解是解题的关键.

练习册系列答案
相关题目
 (2012•恩施州)如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是( )
(2012•恩施州)如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是( ) 如图,菱形ABCD和菱形AEFG开始时互相重合,现将菱形AEFG绕点A顺时针旋转,设旋转角∠BAE=α(0°<α<360°),则当α=
如图,菱形ABCD和菱形AEFG开始时互相重合,现将菱形AEFG绕点A顺时针旋转,设旋转角∠BAE=α(0°<α<360°),则当α= 如图,菱形ABCD和菱形ECGF的边长分别为4和6,∠A=120°,则阴影部分的面积是
如图,菱形ABCD和菱形ECGF的边长分别为4和6,∠A=120°,则阴影部分的面积是