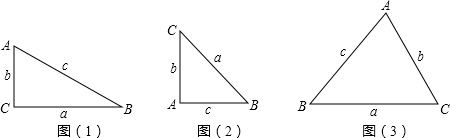
题目内容
3.在等腰直角三角形AOB中,已知AO⊥OB,点P、D分别在AB、OB上,(1)如图1中,若PO=PD,∠OPD=45°,证明△BOP是等腰三角形.
(2)如图2中,若AB=10,点P在AB上移动,且满足PO=PD,DE⊥AB于点E,试问:此时PE的长度是否变化?若变化,说明理由;若不变,请予以证明.
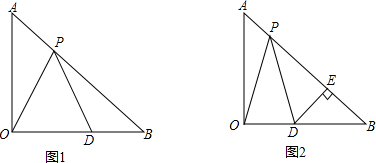
分析 (1)由PO=PD,利用等边对等角和三角形内角和定理可求得∠POD=67.5°,∠OPB=67.5°,然后利用等角对等边可得出结论;
(2)过点O作OC⊥AB于C,首先利用等腰直角三角形的性质可以得到∠COB=∠B=45°,OC=5,然后证得∠POC=∠DPE,进而利用AAS证明△POC≌△DPE,再根据全等三角形的性质可得OC=PE.
解答 (1)证明:∵PO=PD,∠OPD=45°,
∴∠POD=∠PDO=$\frac{180°-∠OPD}{2}$=67.5°,
∵等腰直角三角形AOB中,AO⊥OB,
∴∠B=45°,
∴∠OPB=180°-∠POB-∠B=67.5°,
∴∠POD=∠OPB,
∴BP=BO,即△BOP是等腰三角形;
(2)解:PE的值不变,为PE=5,证明如下:
如图,过点O作OC⊥AB于C,
∵∠AOB=90°,AO=BO,
∴△BOC是等腰直角三角形,∠COB=∠B=45°,点C为AB的中点,
∴OC=$\frac{1}{2}$AB=5,
∵PO=PD,
∴∠POD=∠PDO,
又∵∠POD=∠COD+∠POC=45°+∠POC,∠PDO=∠B+∠DPE=45°+∠DPE,
∴∠POC=∠DPE,
在△POC和△DPE中,
$\left\{\begin{array}{l}{∠PCO=∠DEP=90°}\\{∠POC=∠DPE}\\{PO=DP}\end{array}\right.$,
∴△POC≌△DPE(AAS),
∴OC=PE=5,
∴PE的值不变,为5.
点评 本题考查了等腰三角形的判定与性质,全等三角形的判定与性质,等腰直角三角形等知识,解答(2)的关键是正确作出辅助线,并利用AAS证得△POC≌△DPE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.计算(2a3)2的结果是( )
| A. | 2a5 | B. | 4a5 | C. | 2a6 | D. | 4a6 |
18.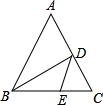 如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
 如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )| A. | AD<DE | B. | AD=DE | C. | AD>DE | D. | 不确定 |
8.下列分解因式,错误的是( )
| A. | m2-16=(m+4)(m-4) | B. | m2+3m+9=(m+3)2 | C. | m2-8m+16=(m-4)2 | D. | m2+4m=m(m+4) |
12.下列去括号正确的是( )
| A. | -(a-b+2c)=-a+b+2c | B. | 3m2-2(m3-m-1)=3m2-2m3+2m+1 | ||
| C. | -(3a-2b)-3(-a2+2b2)=-3a+2b+3a2-6b2 | D. | 3m2+(-5m+2n)-(x-2y)=3m2+5m-2n+x-2y |