题目内容
16.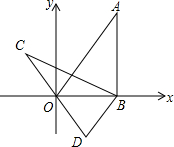 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )| A. | (-2,2$\sqrt{3}$) | B. | (-4,2$\sqrt{3}$) | C. | (-2$\sqrt{3}$,2) | D. | (-2$\sqrt{3}$,4) |
分析 作CH⊥x轴于H点,如图,先求出A点坐标得到AB=4$\sqrt{3}$,再利用旋转的性质得到BC=BA=4$\sqrt{3}$,∠ABC=60°,则∠CBH=30°,然后根据含30度的直角三角形三边的关系,在Rt△CBH中计算出CH和BH,从而可得到C点坐标.
解答 解:作CH⊥x轴于H点,如图,
当x=4时,y=$\sqrt{3}$x=4$\sqrt{3}$,则A(4,4$\sqrt{3}$),
∴AB=4$\sqrt{3}$,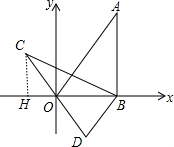
∵△ABO绕点B逆时针旋转60°,得到△CBD,
∴BC=BA=4$\sqrt{3}$,∠ABC=60°,
∴∠CBH=30°,
在Rt△CBH中,CH=$\frac{1}{2}$BC=2$\sqrt{3}$,BH=$\sqrt{3}$CH=6,
∴OH=BH-OB=6-4=2,
∴C点坐标为(-2,2$\sqrt{3}$).
故选A.
点评 本题考查了坐标与图形变换-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.解决本题的关键是旋转的性质的熟练运用.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
5.下列图形是正方体表面积展开图的是( )
| A. |  | B. |  | C. |  | D. |  |

 某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).
某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).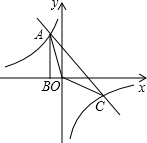 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与y=-x-(k+1)在第二象限的交点,AB⊥x轴于B且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与y=-x-(k+1)在第二象限的交点,AB⊥x轴于B且S△ABO=$\frac{3}{2}$.