题目内容
11.下列图形都是由同样大小的矩形按一定的规律组成,其中,第①个图形中一共有6个矩形,第②个图形中一共有11个矩形,…,按此规律,第⑥个图形中矩形的个数为( )
| A. | 30 | B. | 25 | C. | 28 | D. | 31 |
分析 由于图①有矩形有6个=5×1+1,图②矩形有11个=5×2+1,图③矩形有16=5×3+1,第n个图形矩形的个数是5n+1把n=6代入求出即可.
解答 解:∵图①有矩形有6个=5×1+1,
图②矩形有11个=5×2+1,
图③矩形有16=5×3+1,
…
∴第n个图形矩形的个数是5n+1
当n=6时,5×6+1=31个,
故选:D.
点评 此题主要考查了图形的变化规律,是根据图形进行数字猜想的问题,关键是通过归纳与总结,得到其中的规律,然后利用规律解决一般问题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
2.下列计算结果为正数的是( )
| A. | (-$\frac{1}{2}$)3 | B. | (-$\frac{1}{2}$)-2 | C. | -(-$\frac{1}{2}$)0 | D. | -|$\frac{1}{2}$| |
16.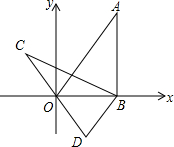 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )| A. | (-2,2$\sqrt{3}$) | B. | (-4,2$\sqrt{3}$) | C. | (-2$\sqrt{3}$,2) | D. | (-2$\sqrt{3}$,4) |
1. 假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是( )
假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是( )
 假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是( )
假如小猫在如图所示的地板上自由地走来走去,并随意停留在某块方砖上,它最终停留在黑色方砖上的概率是( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
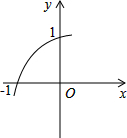 已知函数y=ax2+bx+c的图象的一部分如图所示.该图象过点(-1,0)和(0,1),且顶点在笫一象限,则a+b+c的取值范围是0<a+b+c<2.
已知函数y=ax2+bx+c的图象的一部分如图所示.该图象过点(-1,0)和(0,1),且顶点在笫一象限,则a+b+c的取值范围是0<a+b+c<2.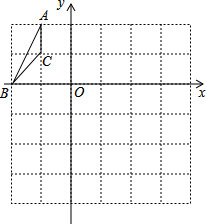 如图,△ABC在平面直角坐标系中,以原点O为位似中心,将△ABC放大到原来的2倍得到△A′B′C′,那么落在第四象限的点A′的坐标是(2,-4).
如图,△ABC在平面直角坐标系中,以原点O为位似中心,将△ABC放大到原来的2倍得到△A′B′C′,那么落在第四象限的点A′的坐标是(2,-4).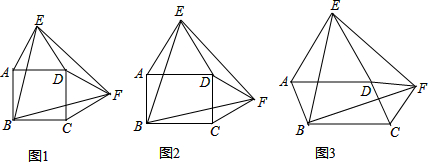
 一个正方形的平面展开图如图所示,将它折成正方体后,“保”字对面的字是碳.
一个正方形的平面展开图如图所示,将它折成正方体后,“保”字对面的字是碳.