题目内容
4.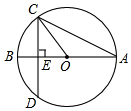 如图,在⊙O中,弦CD垂直直径AB于点E,已知OC=4,CD=4$\sqrt{2}$,则∠BAC的度数为( )
如图,在⊙O中,弦CD垂直直径AB于点E,已知OC=4,CD=4$\sqrt{2}$,则∠BAC的度数为( )| A. | 15° | B. | 22.5° | C. | 30° | D. | 45° |
分析 由垂径定理可得CE=$\frac{1}{2}$CD=2$\sqrt{2}$,然后求出∠COE的正弦值,进而可得∠COE的度数,再根据圆周角定理可得∠BAC的度数.
解答 解:∵CD⊥直径AB,
∴CE=$\frac{1}{2}$CD=2$\sqrt{2}$,sin∠COE=$\frac{CE}{CO}$=$\frac{2\sqrt{2}}{4}$=$\frac{\sqrt{2}}{2}$,
∴∠COE=45°,
∵OA=OC,
∴∠BAC=∠OCA=$\frac{1}{2}$∠COE=22.5°.
故选:B.
点评 此题主要考查了垂径定理和圆周角定理,关键是掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
14. 如图,一个水平放置的六棱柱,这个六棱柱的左视图是( )
如图,一个水平放置的六棱柱,这个六棱柱的左视图是( )
 如图,一个水平放置的六棱柱,这个六棱柱的左视图是( )
如图,一个水平放置的六棱柱,这个六棱柱的左视图是( )| A. |  | B. |  | C. |  | D. |  |
9. 如图是某个几何体的三视图,该几何体为( )
如图是某个几何体的三视图,该几何体为( )
 如图是某个几何体的三视图,该几何体为( )
如图是某个几何体的三视图,该几何体为( )| A. | 长方体 | B. | 四面体 | C. | 圆柱体 | D. | 四棱锥 |
16. 如图,现将一块三角板的含有60°角的顶点放在直尺的一边上,若∠1=2∠2,那么∠1的度数为( )
如图,现将一块三角板的含有60°角的顶点放在直尺的一边上,若∠1=2∠2,那么∠1的度数为( )
 如图,现将一块三角板的含有60°角的顶点放在直尺的一边上,若∠1=2∠2,那么∠1的度数为( )
如图,现将一块三角板的含有60°角的顶点放在直尺的一边上,若∠1=2∠2,那么∠1的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
13.下列调查中,调查方式选择正确的是( )
| A. | 为了了解全市中学生课外阅读情况,选择全面调查 | |
| B. | 端午节期间,我市食品安全检查部门调查市场上粽子的质量情况,选择全面调查 | |
| C. | 旅客上飞机前的安检,选择抽样调查 | |
| D. | 为了了解《人民的名义》的收视率,选择抽样调查 |
14.下列多项式乘法能用平方差公式进行计算的是( )
| A. | (a+b)(b+a) | B. | (a+b)(-a-b) | C. | (a-b)(b-a) | D. | (a-b)(b+a) |