题目内容
3.计算:$\sqrt{({m}^{2}+{n}^{2})^{2}-({m}^{2}-{n}^{2})^{2}}$(m>0,n<0)分析 先将被开方数利用平方差公式进行因式分解,再根据单项式乘单项式的法则计算,得出原式=$\sqrt{({m}^{2}+{n}^{2}+{m}^{2}-{n}^{2})({m}^{2}+{n}^{2}-{m}^{2}+{n}^{2})}$=$\sqrt{2{m}^{2}•2{n}^{2}}$=$\sqrt{4{m}^{2}{n}^{2}}$,然后根据二次根式的性质即可求解.
解答 解:∵m>0,n<0,
∴$\sqrt{({m}^{2}+{n}^{2})^{2}-({m}^{2}-{n}^{2})^{2}}$
=$\sqrt{({m}^{2}+{n}^{2}+{m}^{2}-{n}^{2})({m}^{2}+{n}^{2}-{m}^{2}+{n}^{2})}$
=$\sqrt{2{m}^{2}•2{n}^{2}}$
=$\sqrt{4{m}^{2}{n}^{2}}$
=|2mn|
=-2mn.
点评 本题考查了二次根式的性质与化简,掌握$\sqrt{{a}^{2}}$=|a|及平方差公式是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.已知两直线y1=kx+k-1,y2=(k+1)x+k(k是正整数),设两条直线与x轴围成三角形的面积为Sk,则S1+S2+S3+…+S2014=( )
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2014}{2013}$ | D. | $\frac{1007}{2015}$ |
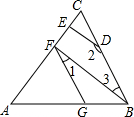 如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,∠FGB=130°,求∠ABC的大小.
如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,∠FGB=130°,求∠ABC的大小.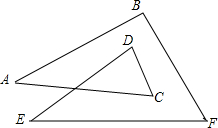 在图中,猜想∠A+∠B+∠C+∠D+∠E+∠F=360°,说明你的理由.
在图中,猜想∠A+∠B+∠C+∠D+∠E+∠F=360°,说明你的理由.